Uraian: Contoh Bilangan Prima (Lengkap)

Contoh Bilangan Prima - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Contoh Bilangan Prima?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Contoh Bilangan Prima ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Contoh Bilangan Prima

Bilangan memiliki beberapa jenis seperti bilangan bulat, cacah, asli, dan bilangan prima yang nantinya akan kita pelajari lebih lanjut.

Sebelum belajar terkait bilangan prima, kalian harus mengetahui apa itu bilangan asli.

Bilangan asli bisa disebut sebagai bilangan bulat positif, contohnya 1, 2, 3, 4, 5, dan seterusnya.

Sementara bilangan prima sendiri ada di dalam bilangan asli tersebut. Lantas bilangan asli seperti apa yang masuk ke dalam bilangan prima?

Untuk menjawab pertanyaan di atas, simak baik – baik ulasan di bawah ini terkait contoh bilangan prima.

Sejarah Singkat Bilangan Prima

Berdasarkan catatan yang ditemukan, diketahui bahwa bilangan prima sudah dipelajari sekitar pada tahun 300 sebelum masehi oleh seorang matematikawan asal Yunani bernama Euclid of Alexandria.

Beliau juga menjadi orang yang menyatakan bahwa bilangan prima tidak terbatas.

Setelah sekitar 100 tahun kemudian, ilmuwan asal Yunani lainnya yang bernama Eratosthenes of Cyrene menemukan adanya metode screening untuk mengidentifikasi bilangan prima.

Selepas studi yang ditempuh oleh ilmuwan Yunani tadi, studi terkait bilangan prima tidaklah terlalu banyak berkembang.

Perkembangan pesat bilangan ini terjadi di abad ke 17 pada saat ada seorang biarawan Prancis uang bernama Marin Mersenne mendefinisikan bilangan prima sebagai berikut ini:

M_p = 2^p – 1

JIka p merupakan bilangan prima, terdapat kemungkinan, walaupun tidak pasti, bahwa M_p merupakan bilangan prima juga.

Sebelumnya, tepatnya di tahun 1588, seorang matematikawan asal Italia yang bernama Pietro Cataldi menjumpai bilangan prima yang menjadi bilangan prima terbesar yang diketahui pada eranya yakni 2¹⁹ – 1 = 524,287.

Sementara untuk angka prima terbesar yang ditemukan dengan cara hitung manual yakni 2¹²⁷ – 1.

Angka yang terdiri atas 39 digit ini dijumpai oleh matematikawan asal Prancis yang bernama Édouard Lucas di tahun 1876.

Studi terkait bilangan prima terus berlanjut hingga pada tahun 1996 didirikanlah the Great Internet Marsenne Prime Search (GIMPS) oleh Gaorge Woltman dari Massachusetts Institute of Technology.

Proyek satu ini didirikan guna mengeksporasi berbagai bilangan prima yang belum ditemukan.

Namun yang menarik, semua orang dapat berpartisipasi di dalam proyek satu ini dengan cara mengunduh software yang sudah disediakan pada website GIMPS.

Dari proyek satu ini, di tahun 2018 ditemukan ada bilangan prima baru yakni 2^77,232,917 – 1 bilangan prima satu ini terdiri dari 23,249,425 digits yang jika ditulis dalam lembaran kertas akan memerlukan kurang lebih 10.000 lembar.

Pengertian Bilangan

Bilangan merupakan suatu konsep matematika yang dipakai di dalam pengukuran serta pencacahan.

Atau secara singkat, bilangan menjadi sebutan dalam menyatakan banyak / jumlah dari sesuatu.

Lambang atau simbol yang dipakai untuk mewakili sebuah bilangan juga bisa disebut sebagai lambang bilangan atau angka.

Pengertian Bilangan Prima

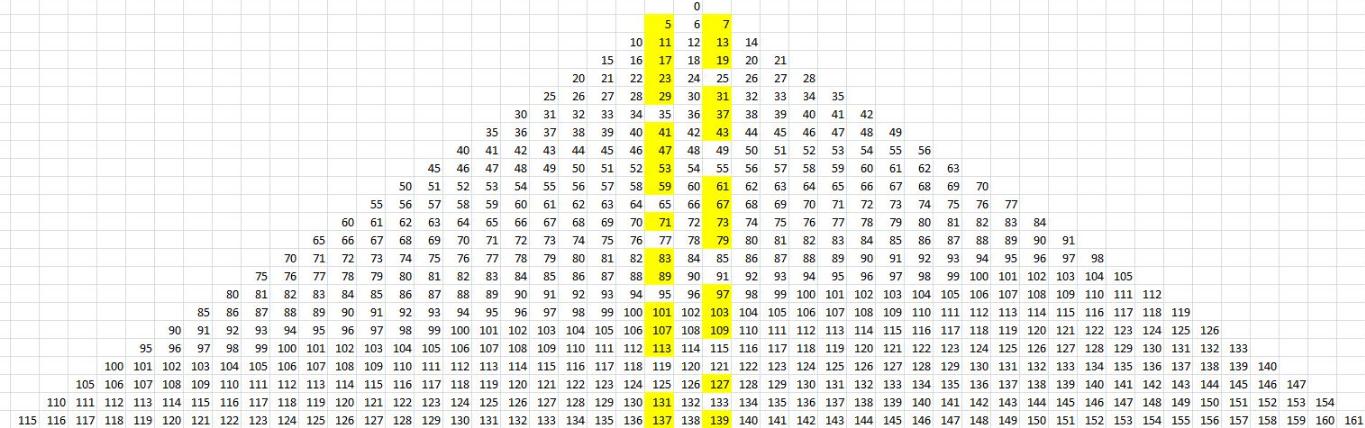
Bilangan prima merupakan bilangan asli yang memiliki nilai lebih dari 1 serta memiliki 2 faktor pembagi yakni 1 dan bilangan itu sendiri.

Jika suatu bilangan memiliki nilai yang lebih besar dari satu, maka bukan disebut sebagai bilangan prima, tetapi bilangan tersebut disebut sebagai bilangan komposit.

Cara yang paling sederhana untuk menentukan bilangan prima yang lebih kecil dari bilangan tertentu ialah dengan memakai saringan Eratosthenes (saringan untuk mencari bilangan prima).

Dengan memakai pengertian di atas, maka bisa kita ketahui bahwa bilangan prima hanya bisa dibagi dengan 2 angka (angka lain & angka itu sendiri).

Bilangan Komposit | Kebalikan Bilangan Prima

Bilangan komposit merupakan kebalikan dari bilangan prima yang mana merupakan bilangan asli bernilai lebih dari 1 dan mempunyai lebih dari 2 faktor pembagi.

Contoh bilangan komposit: 4, 6, 8, dan seterusnya.

Catatan: Angka Negatif, 0, dan 1 bukan termasuk ke dalam bilangan komposit serta bukan termasuk ke dalam bilangan prima.

Hal tersebut disebabkan:

• Angka Negatif bukan merupakan bilangan asli.
• Angka 0 memiliki faktor tak terhingga serta bukan berupa bilangan asli.
• Angka 1 hanya memiliki 1 faktor.

Sehingga dapat kita ketahui, bahwa angka prima dimulai dari 2.

Manfaat Bilangan Prima

Ada dua kegunaan utama pada bilangan prima yang dibagi ke dalam kategori yang berbeda, berikut penjelasannya:

1. Pohon Faktor

Bilangan prima dipakai guna mencari faktor – faktor prima yang ada pada suatu bilangan komposit.

Dari faktor tersebut, dua / lebih bilangan komposit bisa dicari persamaannya lewat Faktor Persekutuan Terbesar (FPB) serta Kelipatan Persekutuan Terkecil (KPK).

a. FPB

FPB berfungsi untuk menyederhanakan pecahan.

Contoh: FPB dari 15 & 35 yaitu 5, sehingga pecahan 15/35 bisa kita sederhanakan dengan cara membagi masing -masing bilangan dengan angka 5, menjadi 3/7.

FPB juga bisa dipakai untuk mencari tahu berapa jumlah maksimum dari penerima yang memperoleh jumlah sama dari setiap barang yang dibagikan di dalam satu paket.

Contoh: Apabila kita mempunyai 12 permen & 8 biskuit yang hendak kita bungkus dengan jumlah merata, maka kita akan memperoleh maksimal 4 bungkus (FPB dari 12 & 8 yaitu 4) yang mana tiap – tiap bungkus terdiri atas 3 permen & 2 biskuit.

b. KPK

KPK berfungsi untuk mencari pertemuan dua bilangan / lebih.

Contoh: Mencari pertemuan antara Ani, Beti, serta Lia di perpustakaan apabila Ani ke perpustakaan setiap 3 hari sekali, Beti setiap 4 hari sekali, serta Lia setiap 7 hari sekali.

KPK dari 3, 4, dan 7 yaitu 84. Artinya ketiganya akan berpapasan di perpustakaan setiap 84 hari sekali.

2. Komputasi

Bilangan prima banyak dipakai untuk kebutuhan enkripsi di dalam komputasi. Bilangan ini dipakai guna membuat kunci dari algoritme pengamanan yang dipakai di internet seperti SHA-256.

Materi Faktor Prima

Faktor prima merupakan suatu bilangan angka prima yang terkandung di dalam faktor pada sebuah bilangan.

Cara dalam mencari faktor prima dari sebuah bilangan bisa dilakukan dengan memakai pohon faktor.

Contoh:

Pada gambar di atas, disajikan proses pemfaktoran dengan memakai pohon faktor agar dapat mengetahui faktor prima dari sebuah bilangan.

Dilihat dari contoh, maka diperoleh bahwa:

• Angka 14 mempunyai faktor prima 2 x 7.
• Angka 40 mempunyai faktor prima 2 x 2 x 2 x 5.

Cara itu bisa kalian lakukan untuk angka lain dengan menggunakan tahapan berikut:

• Bagi angka tersebut dengan menggunakan bilangan prima 2.
• Apabila sudah tidak bisa dibagi dengan angka 2, kalian lanjutkan dengan angka 3.
• Apabila sudah tidak bisa dibagi dengan angka 3, kalian lanjutkan dengan angka 5.
• Dan seterusnya kalian lanjutkan membagi dengan menggunakan bilangan angka prima hingga angka tersebut habis dibagi.

Contoh Bilangan Prima

Berikut ini adalah contoh bilangan prima lengkap yang akan dibagi dalam tiga kelompok untuk memudahkan nya, antara lain:

a. Angka prima di bawah 100

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

b. Angka prima 3 digit (diatas 100)

101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997

c. Angka prima 4 digit (diatas 1000)

1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, dan seterusnya.

d. Angka prima terbesar

Seperti yang telah disebutkan sebelumnya, sebenarnya tidak ada istilah angka prima terbesar, sebab pada dasarnya angka itu tidak terhingga.

Analisa logaritmik pada bilangan prima, yang menunjukkan jika tidak ada bilangan prima terbesar.

Namun terdapat fakta unik dari penelusuran para ilmuwan matematika yang dilakukan pada tahun 2007 lalu, dijumpai adanya bilangan angka prima di nilai 2^23.582.657-1, yang mana bilangan tersebut terdiri dari 9.808.358 digit.

Contoh Soal Bilangan Prima

Untuk lebih mudah memahami uraian di atas, berikut kami berikan beberapa contoh soal terkait bilangan prima, antara lain:

1. Apakah angka 15 adalah bilangan prima?

Jawab:

Angka 15 tidak termasuk ke dalam bilangan prima, sebab memiliki lebih dari 2 faktor yakni 1, 3, 5, 15

1 sebab 15 : 1 = 15
3 sebab 15 : 3 = 5
5 sebab 15 : 5 = 3
15 sebab 15 : 15 = 1

2. Apakah angka 7 adalah bilangan prima?

Jawab:

Angka 7 termasuk ke dalam bilangan prima, sebab hanya memiliki 2 faktor pembagi yakni 1 dan 7

1 sebab 7 : 1 = 7
7 sebab 7 : 7 = 1

Tidak ada angka lain yang dapat membagi habis angka 7.

3. Tentukan faktor prima dari angka 36!

Jawab:

Beriktu cara untuk mencarinya:

• Bagi 36 dengan 2, hasilnya 18.
• Bagi 18 dengan 2, hasilnya 9.
• Angka 9 tidak dapat dibagi dengan 2, maka dilanjutkan dengan menggunakan angka prima 3
• Bagi 9 dengan 3, sehingga hasil akhir menyisakan 3.

Dari cara tersebut, maka dapat diketahui bahwa faktor prima dari 36 yaitu 2 x 2 x 3 x 3.

4. Apakah 1 bilangan prima?

Jawab:

Angka 1 bukan merupakan bilangan prima sebab hanya mempunyai 1 faktor saja.

5. Sebutkan bilangan prima genap?

Jawab:

Ada satu bilangan prima genap, yakni angka 2. Bilangan satu ini sekaligus menjadi bilangan prima yang terkecil.

6. Tentukan faktor prima dari 45!

Jawab:

Berikut akan menggunakan gambar pemfaktoran supaya lebih jelas:

Dari pohon faktor di atas, maka diketahui bahwa faktor prima dari 45 yaitu 3 x 3 x 5.

The post Contoh Bilangan Prima appeared first on Yuksinau.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Contoh Bilangan Prima (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.