Uraian: Pertidaksamaan Linear Dua Variabel (SPtLDV) (Lengkap)

Pertidaksamaan Linear Dua Variabel (SPtLDV) - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Pertidaksamaan Linear Dua Variabel (SPtLDV)?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Pertidaksamaan Linear Dua Variabel (SPtLDV) ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Pertidaksamaan Linear Dua Variabel (SPtLDV)

Pertidaksamaan Linear Dua Variabel (SPLDV)-  merupakan suatu kalimat terbuka matematika yang di dalamnya memuat dua variabel.

Dengan masing-masing variabel berderajat satu serta dihubungkan dengan tanda ketidaksamaan. Tanda ketidaksamaan yang dimaksud disini antara lain: >, <, ≤, atau ≥.

Maka, bentuk dari pertidaksamaan linear bisa kita tuliskan seperti berikut ini:

• ax + by > c
• ax + by < c
• ax + by ≥ c
• ax + by ≤ c

Berikut ini adalah contoh dari kalimat matematikanya:

2x + 3y > 6
4x – y < 9

Beberapa kalimat terbuka di atas menggunakan tanda hubung seperti <, >, > atau <. Yang menandakan kalimat tersebut merupakan  pertidaksamaan.

Pertidaksamaan Linear Dua Variabel (SPLDV)

Berbeda halnya dengan penyelesaian dari persamaan linear dua variabel yang berwujud himpunan pasangan titik-titik.

Atau apabila kita gambar grafiknya akan berupa garis lurus.

Penyelesaian dari pertidaksamaan linear dua variabel berupa daerah penyelesaian.

Dalam praktiknya penyelesaian pertidaksamaan linear bisa berwujud daerah diarsir atau sebaliknya daerah penyelesaian pertidaksamaan linear dua variabel yang berupa daerah bersih.

Untuk menentukkan daerah penyelesaiannya, kita bisa melakukan langkah-langkah seperti di bawah ini:

1. Ubahlah tanda ketidaksamaan dari pertidaksamaan menjadi tanda sama dengan (=), sehingga kita akan memperoleh persamaan linear dua variabel
2. Gambar dari grafikatau garis dari persamaan linear dua variabel tadi.
   Hal ini bisa kita lakukan dengan cara menentukan titik potong sumbu x dan sumbu y dari persamaan.
   Ataupun dapat memakai dua titik sembarang yang dilewati oleh garis. Garis akan membagi dua bidang kartesius
3. Lakukan uji titik yang tidak dilewati oleh garis (substitusi nilai x dan y titik ke pertidaksamaan). Apabila menghasilkan pernyataan yang benar, artinya daerah tersebut adalah penyelesaiannya.
   Tetapi, jika menghasilkan pernyataan salah maka bagian lainnya lah yang merupakan penyelesaiaanya.

Untuk lebih jelasnya perhatikan ulasan berikut ini.

Sistem Pertidaksamaan Linear Dua Variabel

Pertidaksamaan linear merupakan pertidaksamaan yang mana peubah bebasnya berbentuk linear (pangkat satu). Kalian tentunya masih ingatkan beberapa kalimat matematika di bawah ini.

• 2x ≥ 4; pertidaksamaan linear satu peubah
• 3x + y < 0; pertidaksamaan linear dua peubah
• x – 2y ≤ 3; pertidaksamaan linear dua peubah
• x + y – 2z > 0; pertidaksamaan linear tiga peubah

Dan kali ini, kami akan membahas seputar pertidaksamaan linear dengan dua peubah.

Gabungan dari dua atau lebih pertidaksamaan linear dua peubah disebut sebagai sistem pertidaksamaan linear dua peubah.

Berikut adalah contoh dari sistem pertidaksamaan linear dua peubah:

3x + 8y ≥ 24,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.

Baca juga: Aljabar

1. Daerah Himpunan Penyelesaian Pertidaksamaan Linear Dua Peubah

Penyelesaian suatu pertidaksamaan linear dua peubah merupakan pasangan berurut (x,y) yang dapat memenuhi pertidaksamaan linear tersebut.

Himpunan dari penyelesaian tersebut dapat dinyatakan dengan sebuah daerah pada bidang kartesius (bidang XOY) yang diarsir.

Untuk lebih memahami daerah himpunan dari penyelesaian pertidaksamaan linear dua peubah. Berikut akan kami berikan contohnya:

Contoh:

Tentukan himpunan penyelesaian dari pertidaksamaan linear di bawah ini:
a. 2x + 3y ≥ 12             c. 4x – 3y < 12
b. 2x – 5y > 20            d. 5x + 3y ≤ 15

Jawab:

a. Langkah pertama adala lukis garis 2x + 3y = 12 dengan cara menghubungkan titik potong garis dengan sumbu X dan sumbu Y.

Titik potong garis dengan sumbu X memilki arti sebagai y = 0, dan didapatkan x = 6 (titik (6,0)).

Titik potong garis dengan sumbu Y artinya x = 0, didapat y = 4 (titik (0,4)).

Garis 2x + 3y = 12 tersebut kemudian akan membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian, maka dilakukan dengan mengambil salah satu titik uji dari salah satu sisi daerah.

Sebagai contoh disini kita ambil titik (0,0). Lalu disubstitusikan ke pertidaksamaan sehingga akan kita peroleh:

2 x0 + 3x 0 < 12
0 < 12

Sehingga, 0 ≥ 12 salah, yang berarti tidak dipenuhi sebagai daerah penyelesaian.

Jadi, daerah penyelesaiannya yaitu daerah yang tidak masuk dalam titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

b. Langkah pertama adalah menggambar garis 2x – 5y = 20 dengan cara menghubungkan titik potong garis di sumbu X dan sumbu Y.

• Titik potong garis dengan sumbu X,  y = 0, didapat x = 10 (titik (10,0))
• Titik potong garis dengan sumbu Y, x = 0, didapat y = –4 (titik (0,–4))

Garis 2x – 5y = 20 tersebut akan membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil titik uji pada salah satu sisi daerah.

Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:

2 x0 – 5 x0 > 20
0 > 20 (salah), artinya tidak dipenuhi.

Sehingga, daerah penyelesaiannya yaitu daerah yang tidak masuk dalam titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

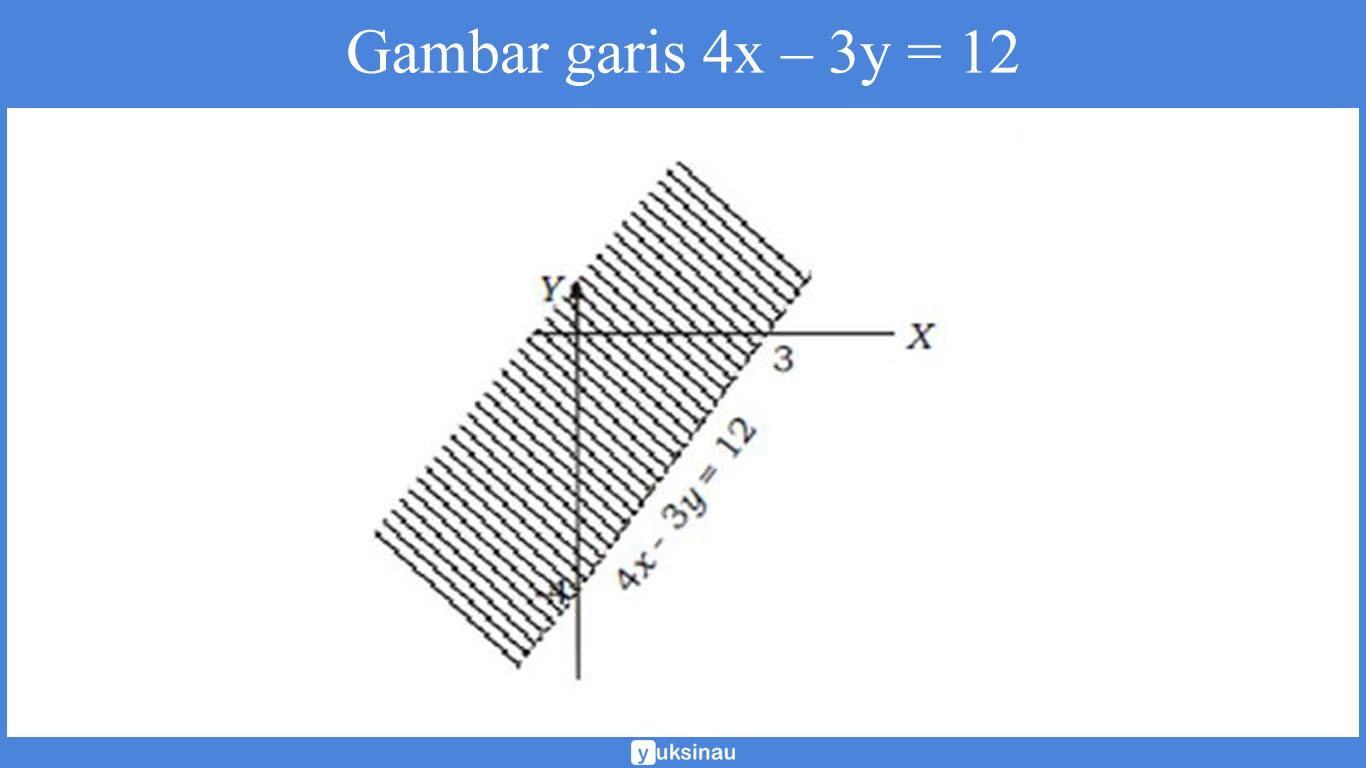
c. Langkah pertama adalah menggambar garis 4x – 3y = 12 dengan cara menghubungkan titik potong garis pada sumbu X dan sumbu Y.

• Titik potong garis dengan sumbu X maka y = 0 didapat x = 3 (titik (3,0))
• Titik potong garis dengan sumbu Y maka x = 0 didapat y = –4 (titik (0,–4))

Garis 4x – 3y = 12 tersebut akan membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil salah satu titik uji dari salah satu sisi daerah.

Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:

4 x0 – 3x 0 < 12
0 < 12 (benar), yang berarti dipenuhi sebagai daerah penyelesaian.

Sehingga, daerah penyelesaiannya yaitu daerah yang terdapat atau memuat titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

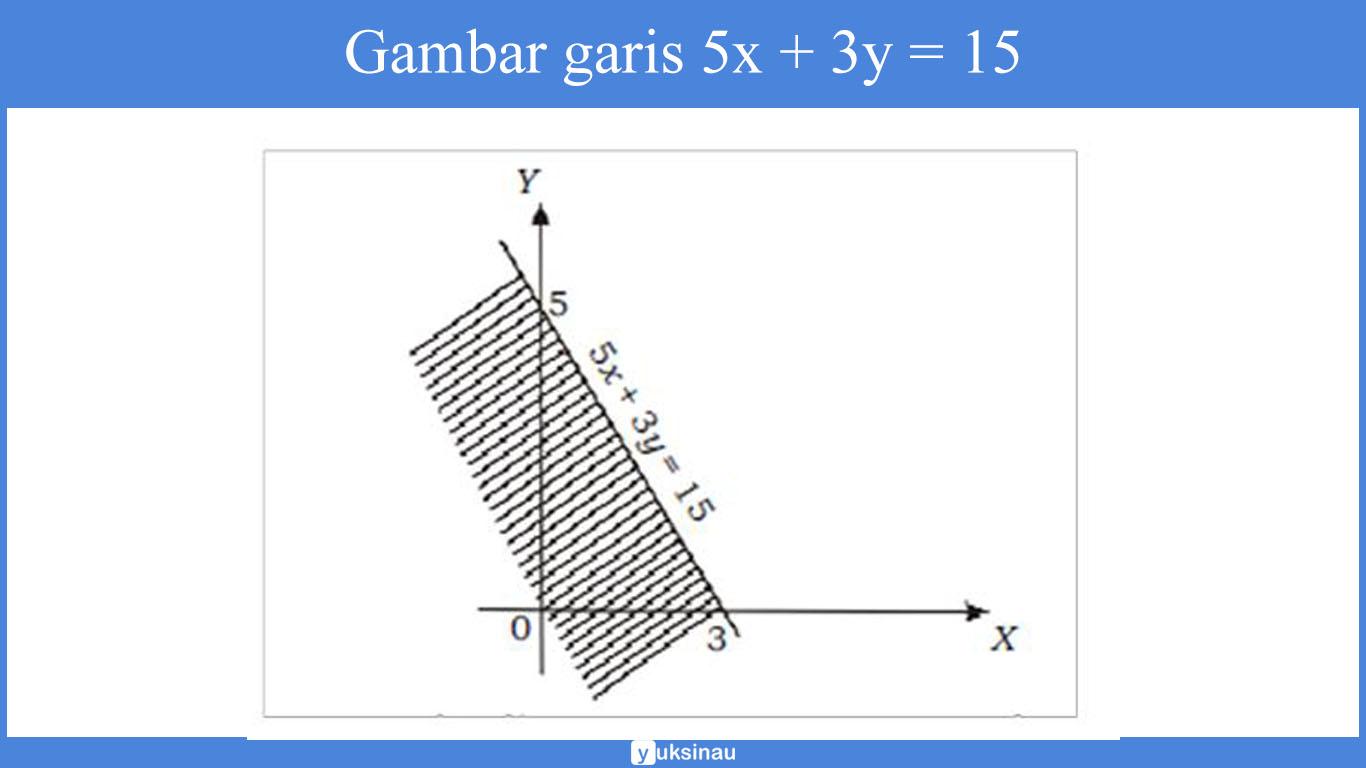
d. Langkah pertama adalah menggambar garis 5x + 3y = 15 dengan cara menghubungkan titik potong garis pada sumbu X dan sumbu Y.

• Titik potong garis dengan sumbu X maka y = 0, didapat x = 3 (titik (3,0))
• Titik potong garis dengan sumbu Y maka x = 0, didapat y = 5 (titik (0,5))

Garis 5x + 3y = 15 tersebut membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil salah satu titik uji dari salah satu sisi daerah.

Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:

5 x0 + 3x 0 ≤15
0 ≤ 15 (benar), artinya dipenuhi.

Sehingga, daerah penyelesaiannya yaitu daerah yang terdapat atau memuat titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

Berdasarkan dari contoh di atas, cara untuk menentukan himpunan penyelesaian pertidaksamaan linear dengan dua peubah bisa kila laukan dengan beberapa langkah seperti di bawah ini:

1. Menggambar garis ax + by = c dalam bidang kartesius dengan cara menghubungkan titik potong garis pada sumbu X di titik (c/a ,0) serta pada sumbu Y di titik (0,c/b ).

2. Kita cari tahu sebuah titik uji yang berada di luar garis dengan cara menyubstitusikannya pada pertidaksamaan.

Apabila pertidaksamaan mampu terpenuhi (benar), maka daerah yang memuat titik tersebut adalah daerah himpunan penyelesaian.

Apabila pertidaksamaan tidak dipenuhi (salah), maka daerah yang tidak terdapat pada titik uji tersebut adalah daerah himpunan penyelesaian.

2. Daerah Penyelesaian Sistem Pertidaksamaan Linear

Himpunan penyelesaian sistem pertidaksamaan linear dua peubah merupaan himpunan titik-titik (pasangan berurut (x,y)) dalam bidang kartesius yang dapat memenuhi seluruh pertidaksamaan linear dalam sistem tersebut.

Sehingga daerah himpunan penyelesaiannya adalah irisan dari beberapa himpunan penyelesaian dari pertidaksamaan dalam sistem pertidaksamaan linear dua peubah itu.

Supaya kalian lebih mudah untuk memahami daerah penyelesaian dari sistem pertidaksamaan linear dua peubah, perhatikan beberapa contoh yang akan kami sajikan di bawah ini.

Contoh:

Tentukan daerah himpunan penyelesaian dari sistem pertidaksamaan di bawah ini:
a. 3x + 5y ≤ 15               b. x + y ≤ 6
x ≥ 0                                    2x + 3y ≤ 12
y ≥ 0                                    x ≥ 1
y ≥  2

Jawab:

a. Langkah pertama adalah menggambar garis 3x + 5y =15, x = 0, dan y =0

Untuk 3x + 5y ≤ 15

Kemudian pilih titik (0,0), lalu kita substitusikan ke pertidaksamaan sehingga akan kita dapatkan:
3x 0 + 5x 0 ≤ 15
0 ≤ 15 (benar), yang berarti dipenuhi

Sehingga, daerah penyelesaiannya yaitu daerah yang memuat titik (0,0)

Untuk x ≥ 0, kita pilih titik (1,1) lalu disubstitusikan ke pertidaksamaan sehingga akan kita dapatkan:
1 ≥ 0 (benar), yang berarti dipenuhi.

Sehingga, daerah penyelesaiannya ialah daerah yang memuat titik (1,1)
Untuk y ≥ 0, kita pilih titik (1,1) lalu substitusikan ke dalam pertidaksamaan sehingga akan kita dapatkan:
1 ≥ 0 (benar), yang berarti dipenuhi.

Sehingga, himpunan penyelesaian dari soal tersebut adalah daerah yang memuat titik (1,1).

Daerah himpunan penyelesaian sistem pertidaksamaan adalah irisan dari ketiga daerah himpunan penyelesaian pertidaksamaan di atas.

Yakni yang tertera seperti pada gambar berikut ini (daerah yang diarsir).

b. Langkah pertama adalah menggambar garis x + y =6, 2x + 3y = 12, x = 1, dan y = 2.

Untuk x + y ≤ 6, kita pilih titik (0,0), lalu kita substitusikan ke pertidaksamaan sehingga akan kita dapatkan:

1 x0 + 1 x0 ≤ 6
0 ≤ 6 (benar), yang berarti dipenuhi.

Sehingga, daerah penyelesaiannya yaiu daerah yang memuat titik (0,0).
Untuk 2x + 3y ≤ 12, pilih titik (0,0), lalu kita substitusikan ke pertidaksamaan sehingga akan kita dapatkan:

2 x0 + 3x 0 ≤ 12
0 ≤ 12 (benar), yang berarti dipenuhi.

Sehingga dapat kita ketahui daerah penyelesaiannya yaitu daerah yang memuat titik (0,0).

Untuk x ≥ 1, pilih titik (2,1) lalu kita substitusikan ke pertidaksamaan sehingga kita dapatkan 2 ≥ 1 (benar) yang berarti dipenuhi.

Sehingga, daerah penyelesaiannya yaitu daerah yang memuat titik (2,1).

Untuk y ≥ 2, kita pilih titik (1,3) lalu disubstitusikan ke pertidaksamaan sehingga akan kita peroleh 3 ≥ 2 (benar) yang berarti dipenuhi.

Sehingga, himpunan penyelesaiannya berada di daerah yang memuat titik (1,3).

Daerah himpunan penyelesaian dari sistem pertidaksamaan tersebut adalah irisan dari ketiga daerah himpunan penyelesaian pertidaksamaan di atas.

Seperti yang terlihat pada gambar di samping (daerah yang diarsir).

b. Menentukan Sistem Pertidaksamaan jika Daerah Himpunan Penyelesaian Sistem Pertidaksamaan Linear Dua Peubah Diketahui

Cara menentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah sudah kita pelajari di baba sebelumnya.

Sekarang bagaimana cara untuk menentukan sistem pertidaksamaan apabila daerah himpunan penyelesaiannya yang diketahui?

Simak penjelasannya berikut ini.

Contoh:

Daerah yang diarsir di bawah ini adalah daerah himpunan penyelesaiaan dari sebuah sistem pertidaksamaan linear dua peubah.

Maka, tentukanlah sistem pertidaksamaan tersebut.

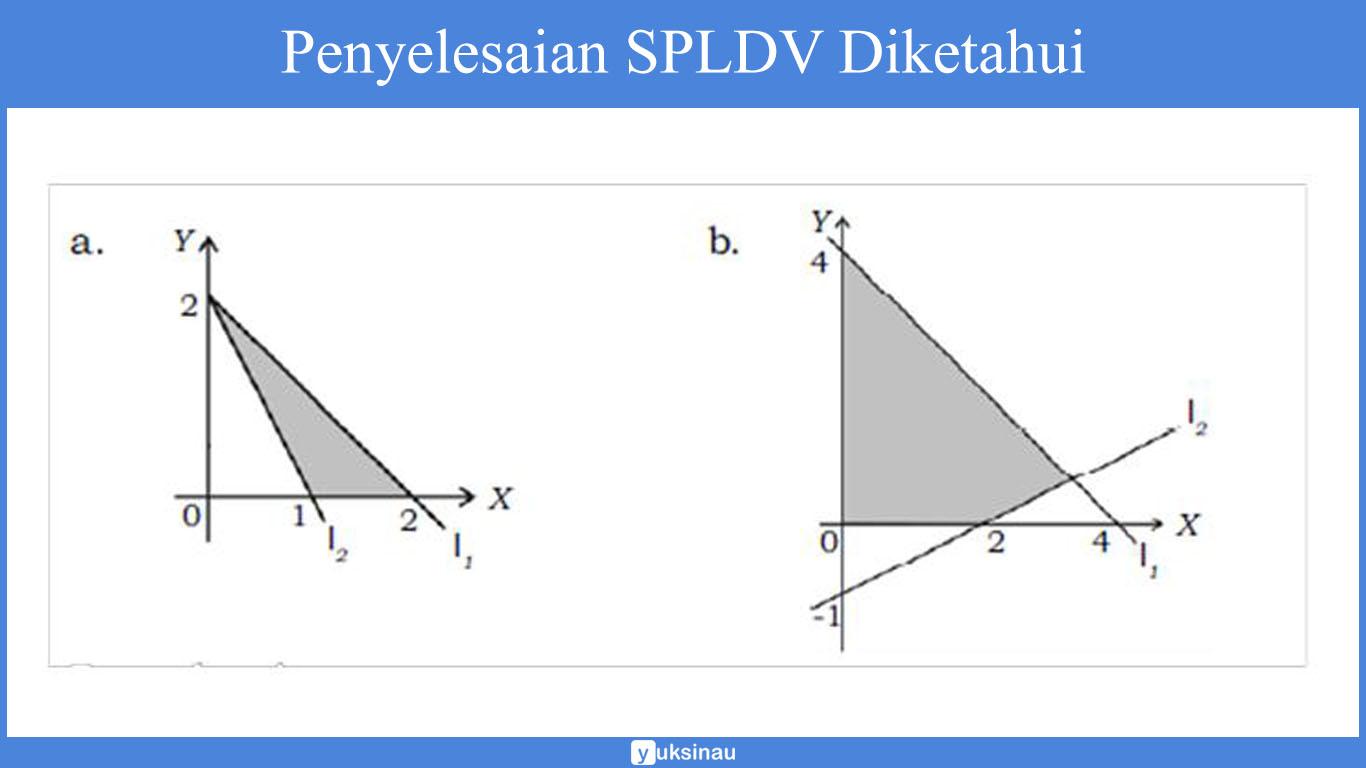
Jawab:

a. Garis l1 melalui titik (2,0) dan (0,2), persamaan garis l1 yaitu:

x/2 + y/2 = 1 menjadi x+y=2

Garis l2 melaui titik (1,0) dan (0,2), persamaan garis l2 yaitu:

x/1 + y/2 = 1 menjadi 2x+y=2

Dari gambar di atas, diketahui bahwa daerah himpunan penyelesaian (yang diarsir) terletak di bawah garis l1, di atas garis l2, di kanan sumbu Y, dan di atas sumbu X. Sistem pertidaksamaannya yakni:

x + y ≤ 2, 2x + y ≥ 2, x ≥ 0, dan y ≥  0

b. Garis l1 melalui titik (4,0) dan (0,4), persamaan garis l1 yaitu:

x/4 + y/4 = 1 menjadi x+y=4

Garis l2 melalui titik (2,0) dan (0,–1), persamaan garis l2 yaitu:

x/2 + y/-1 = 1 menjadi -x+2y = -2

x-2y  = 2

Dari gambar di atas, diketahui bahwa daerah himpunan penyelesaian (yang diarsir) terletak di bawah garis l1, di atas garis l2, di kanan sumbu Y, dan juga di atas sumbu X. Sistem pertidaksamaannya yakni:

x + y ≤ 4, x – 2y ≤ 2, x ≥ 0, dan y ≥ 0

Contoh Soal Cerita

Berikut akan kami berikan contoh dari soal cerita Sistem Persamaan Linear Dua Variabel (SPLDV) dalam kehidupan sehari-hari kehidupan sehari-hari yang diambil dari soal-soal Ujian Nasional.

Soal 1 (UN 2016)

Seorang tukang parkir mendapat uang sebesar Rp17.000,00 dari 3 buah mobil dan 5 buah motor, sedangkan dari 4 buah mobil dan 2 buah motor ia mendapat uang Rp18.000,00. Jika terdapat 20 mobil dan 30 motor, banyak uang parkir yang diperoleh adalah….

A. Rp135.000,00

B. Rp115.000,00

C. Rp110.000,00

D. Rp100.000,00

Jawab:

Misalkan:

Mobil = x dan motor = y

Ditanyakan: 20x + 30y = ….?

Model matematika:
3x + 5y = 17.000  ……(1)
4x + 2y = 18.000  ……(2)

Eliminasi persamaan (1) dan (2) akan didapatkan:

3x + 5y =17.000 | x4 |12x + 20y = 68.000
4x + 2y =18.000 | x3 |12x + 6y = 54.000 –
⟺ 14y = 14.000
⟺ y = 14.000/14
⟺ y = 1.000

Subtitusi nilai y = 1.000 ke salah satu persamaan:

3x+ 5y = 17.000
⟺ 3x + 5(1.000) = 17.000
⟺ 3x + 5.000 = 17.000
⟺ 3x = 17.000 – 5.000
⟺ 3x = 12.000
⟺ x = 12.000/3
⟺ x = 4.000

Maka, biaya parkir 1 mobil Rp4.000,00  dan 1  motor Rp1.000,00
20x + 30y = 20(4.000) + 30(1.000)
= 80.000 +  30.000
= 110.000

Sehingga, banyak uang parkir yang didapatkan sebesar Rp110.000,00
(Jawaban: C)

Soal 2 (UN 2015)

Di dalam kandang terdapat kambing dan ayam sebanyak 13 ekor. Jika jumlah kaki hewan tersebut 32 2kor, maka jumlah kambing dan ayam masing-masing adalah….

A. 3 dan 10

B. 4 dan 9

C. 5 dan 8

D. 10 dan 3

Jawab:

Misalkan:

Kambing = x dan ayam = y

Jumlah kaki kambing = 4 dan kaki ayam = 2

Ditanyakan: Jumlah kambing dan ayam = …?

Model matematika:
x +   y = 13  ……(1)
4x + 2y = 32  ……(2)

Eliminasi persamaan (1) dan (2) akan kita dapatkan:
x +   y = 13 | x4 | 4x + 4y = 52
4x + 2y = 32 | x1 | 4x + 2y = 32 –
⟺ 2y = 20
⟺ y = 20/2
⟺ y = 10
Subtitusi nilai y = 10 ke salah satu persamaan:
x + y = 13
⟺ x + 10 = 13
⟺ x = 13 –  10
⟺ x = 3

Sehingga, jumlah kambing = 3 ekor dan ayam = 10 ekor.
(Jawaban : A)

Baca juga: Pertidaksamaan Linear Satu Variabel (PtLSV)

Demikianlah ulasan singkat terkait Pertidaksamaan Linear Dua Variabel (SPLDV) yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.

The post Pertidaksamaan Linear Dua Variabel (SPtLDV) appeared first on Yuksinau.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Pertidaksamaan Linear Dua Variabel (SPtLDV) (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.