Uraian: Kaidah Pencacahan (Lengkap)
Namun tak ada salahnya sebelum membaca ulasan tentang Kaidah Pencacahan ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?
Pembahasan Lengkap Kaidah Pencacahan
Kaidah pencacahan atau dalam bahasa inggris disebut sebagai (Counting Rules) merupakan sebuah cara atau aturan untuk menghitung seluruh kemungkinan yang bisa terjadi dalam suatu percobaan tertentu.
Kaidah Pencacahan
Kaidah pencacahan merupakan sebuah aturan membilang untuk mengetahui banyaknya kejadian atau objek-objek tertentu yang muncul. Disebut sebagai pencacahan sebab hasilnya berwujud suatu bilangan cacah.
Adapun beberapa metode pada kaidah pencacahan antara lain yaitu: metode aturan pengisian tempat (Filling Slots), metode permutasi serta metode kombinasi. Berikut penjelasannya lebih lanjut.
Aturan Pengisian Tempat
Sebagai contoh ada suatu kasus di bawah ini:
Gilang memiliki 3 kaos dengan warna putih, merah dan biru dan juga memiliki 2 celana panjang yang berwarna hitam dan cokelat.
Tentukan beberapa kemungkinan Gilang akan menggunakan kaos dan juga celana panjang!
Penyelesaian:
Ada 3 cara untuk menentukan berbagai kemungkinan Gilang menggunakan kaos dan celana panjang.
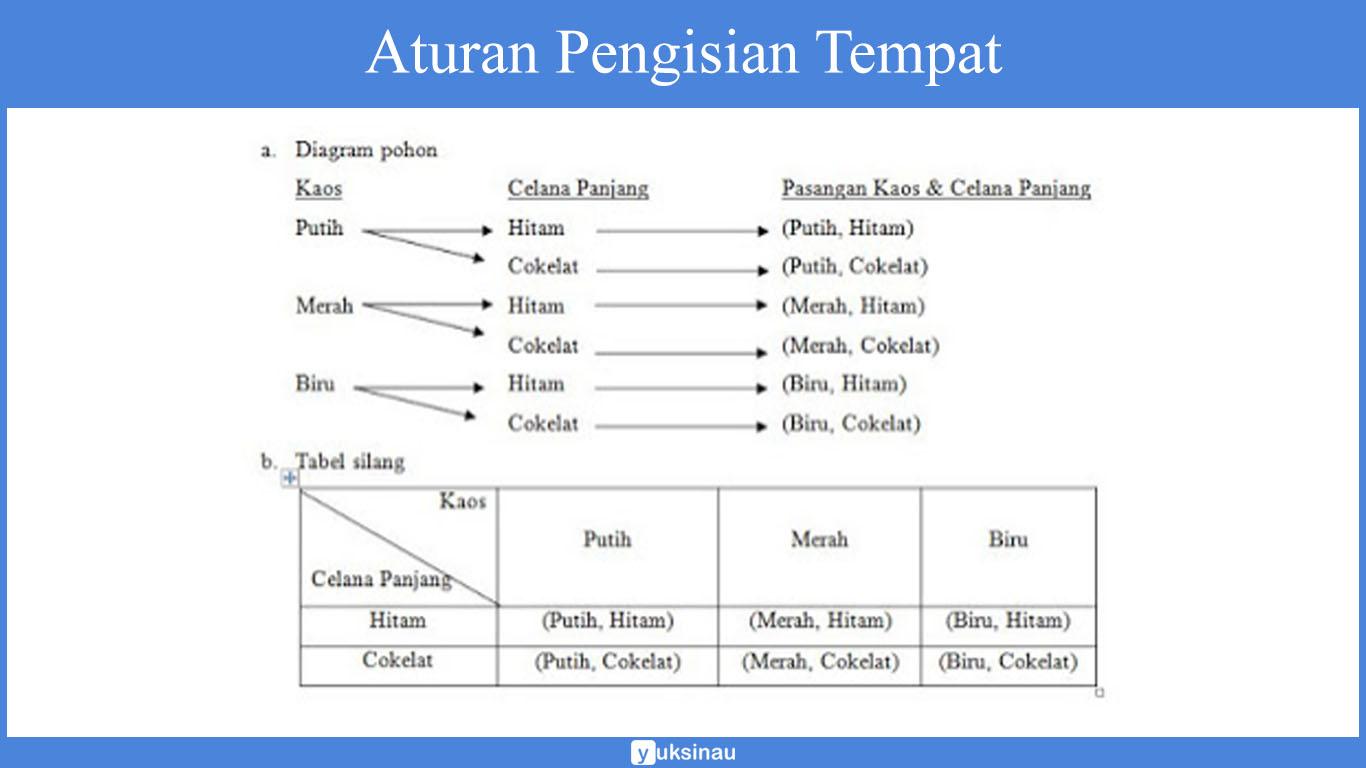
c. Himpunan pasangan terurut
{(Putih, Hitam), (Putih, Cokelat), (Merah, Hitam), (Merah, Cokelat), (Biru, Hitam), (Biru, Cokelat)}
Dari ketiga metode atau cara di atas, bisa kita simpulkan bahwa banyaknya cara Gilang memakai kaos dan juga celana panjang ada sebanyak 6 cara = 3 × 2 = banyak cara menggunakan kaos × banyak cara menggunakan celana
panjang.
Aturan Perkalian
Apabila sebuah kejadian bisa berlangsung dalam n tahap yang saling berurutan di mana tahap 1 bisa berlangsung dalam q1 cara, tahap 2 bisa berlangsung dalam q2 cara, tahap 3 dapat terjadi dalam q3 cara demikian seterusnya hingga tahapan ke – n bisa berlangunsg dalam qncara maka kejadian tersebut bisa terjadi secara berurutan dalam q1 × q2 × q3 × … × qn dengan cara berbeda.
Sebagai contoh:
Berapa banyaknya cara atau metode untuk memilih 3 pengurus OSIS yang terdiri atas ketua, sekretaris serta bendahara dari total 8 orang siswa?
Penyelesaian:
Misal ada 3 tempat untuk mengisi posisi ketua, sekretaris dan bendahara yang kita visualkan seperti di bawah ini:
Ketua Sekretaris Bendahara
Dari ke-8 siswa itu, seluruh berhak dipilih untuk menjadi ketua sehingga terdapat 8 cara untuk mengisi posisi ketua.
Sebab 1 orang telah menjadi ketua maka tinggal 7 orang yang berhak untuk dipilih menjadi sekretaris sehingga terdapat 7 cara untuk mengisi posisi sekretaris.
Sebab 1 orang telah terpilih menjadi ketua serta 1 orang sudah menjadi sekretaris maka tinggal 6 orang yang berhak untuk dipilih menjadi bendahara sehingga terdapat 6 cara untuk mengisi bendahara.
Ilustrasi seperti tabel di bawah ini:
| 8 | 7 | 6 |
Ketua Sekretaris Bendahara
Banyak cara untuk memilih 3 pengurus OSIS tersebut yaitu 8 × 7 × 6 = 336
Aturan Penjumlahan
Sebagai contoh ada sebuah kejadian yang bisa terjadi dalam n cara yang berlainan (saling asing) di mana dalam cara pertama ada p1 kemungkinan hasil yang berbeda.
Pada cara kedua ada p2 kemungkinan hasil yang berbeda. Pada cara ketiga ada p3kemungkinan hasil yang berbeda.
Serta demikian selanjutnya hingga cara yang ke – n ada pn kemungkinan hasil yang berbeda. Sehingga total banyak kemungkinan kejadian dalam peristiwa tersebut yaitu p1 + p2 + p3 + … + pn dengan cara berbeda.
Sebagai contoh:
Putra seorang pelajar SMK swasta di Purwokerto. Putra memiliki tiga jenis alat transportasi yang ia kendarai dari rumah ke sekolah. Antara laing: sepeda (sepeda mini, sepeda gunung), sepeda motor (yamaha, honda, suzuki) serta mobil (sedan, kijang, pick-up).
Pertanyaannya, berapa banyak cara Putra untuk berangkat dari rumah ke sekolah?
Penyelesaian:
Alat transportasi yang dipakai oleh Putra dari rumah ke sekolah hanyalah salah satu saja yakni sepeda atau sepeda motor atau mobil.
Tidak mungkin Putra mengendarai lebih dari satu kendaraan dalam waktu bersamaan. Banyaknya cara Putra berangkat dari rumah ke sekolah merupakan banyak cara mengendarai sepeda + banyak cara mengenadari sepeda motor + banyak cara mengendarai mobil = 2 + 3 + 3 = 8 cara.
Notasi Faktorial
Contohnya n ∈ himpunan bilangan asli. Notasi n! (dibaca: n faktorial) diartikan sebagai hasil kali dari bilangan-bilangan asli secara berurutan dari n sampai 1.
Maka kita tulis:
n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1.
Diartikan sebagai 1! = 1 dan 0! = 1.
Sebagai contoh:
1. Tentukan nilai dari 5!.
Jawab:
5! = 5 × 4 × 3 × 2 × 1 = 120.
2. Tentukan nilai dari 2! + 3!.
Jawab:
2! + 3! = (2 × 1) + (3 × 2 × 1) = 2 × 6 = 12
Permutasi
Materi pertama yang akan kita bahas pada artikel ini adalah permutasi. Permutasi mempelajari mengenai menyusun k objek dari n objek dengan cara memperhatikan urutan.
Ada tiga contoh permutasi yang sering timbul antara lain: permutasi dari unsur-unsur yang berbeda, permutasi dengan beberapa unsur yang sama, serta permutasi siklis. Selengkapnya simak baik-baik ulasan berikut ini.
Macam dan Formula atau Rumus Permutasi
1. Permutasi dari n elemen, masing-masing permutasi terdiri atas n elemen
Apabila terdapat unsur yang berbeda dan diambil n unsur, maka banyaknya susunan atau permutasi yang berbeda dari n unsur tersebut merupakan P(n,n) = n! atau nPn = n!
Sebagai contoh:
Untuk menyambut suatu pertemuan delegasi negara yang dihadiri oleh lima negara. Panitia kemudian akan memasang kelima bendera yang merupakan bendera dari lima negara yang hadir.
Banyak cara untuk panitia menyusun kelima bendera tersebut yaitu?
Jawab:
Dari kelima bendera yang ada, berarti kita peroleh n = 5, sehingga banyak susunan bendera yang mungkin yakni:
5! = 5.4.3.2.1 = 120 cara.
2. Permutasi n elemen, masing-masing permutasi terdiri atas r unsur dari n elemen dengan r ≤ n
Untuk semua bilangan positif n dan r, dengan r≤n, banyaknya permutasi dari n objek yang diambil r objek pada satu waktu adalah:

Catatan:
Syarat: urutan harus diperhatikan.
Sebagai contoh:
Banyak cara untuk memilih seorang ketua, sekertaris dan juga bendahara dari 8 siswa yang tersedia yaitu…
Jawab:
Banyak siswa, n = 8
Ketua, sekretaris serta bendahara (banyak pilihan objek), r = 3
Sehingga:

3. Permutasi dari n unsur yang mengandung p.q dan r unsur yang sama

Keterangan:
n = menunjukan banyaknya elemen seluruhnya
k1 = menunjukan banyaknya elemen kelompok 1 yang sama
k2 = menunjukan banyaknya elemen kelompok 2 yang sama
…
kt = menunjukan banyaknya elemen kelompok kt yang sama
t = 1,2,3,…
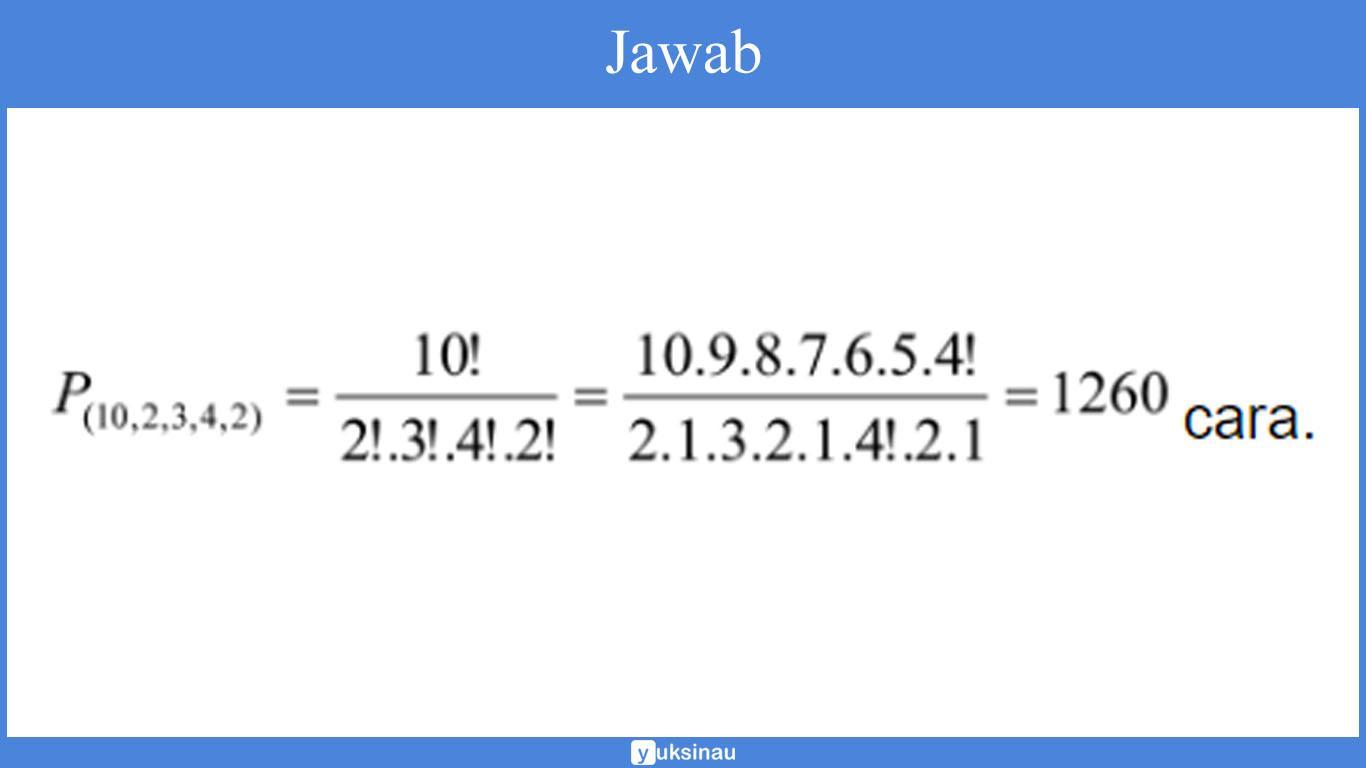
Sebagai cottoh:
Banyaknya cara penyusunan untuk kata ”BASSABASSI” yaitu…
Jawab:
Dari kata ”BASSABASSI”, banyak huruf adalah (n) = 10
k1 = huruf B = 2
k2 = huruf A = 3
k3 = huruf S = 4
k4 = huruf I = 1
4. Permutasi Siklis
Permutasi siklis merupakan suatu permutasi melingkar (urutan melingkar).
Atau sebuah cara atau metode guna menentukan susunan unsur yang disusun secara siklis atau melingkar dengan cara memperhatikan urutannya. Banyaknya permutasi siklis dari n unsur berbeda yaitu:
nPsiklis = (n-1)!
Sebagai contoh:
Dari 5 orang anggota keluarga akan segera duduk mengelilingi satu meja bundar, banyaknya cara penyusunan yang bisa dibikin dari 5 orang tersebut yaitu…
Jawab:
Banyak orang (n) = 5, sehingga:
5Psiklis = (5 – 1)! = 4! = 4.3.2.1 = 24 cara.
5. Permutasi berulang dari n unsur, tipe permutasi terdiri dari k unsur
Pn = nk
Contoh:
Banyak susunan dari 3 bilangan angka-angka 1, 2, 3, 4, 5 dan 6 yaitu…
Jawab:
- Banyaknya susunan 3 bilangan, yang artinya bilangan ratusan, k = 3
- Banyak angka yang akan disusun adalah n = 6
- Banyak susunan 3 bilangan dari angka 1, 2, 3, 4, 5, serta 6, sehingga:
P6 = 63 = 216 susunan.
Kombinasi
Kombinasi merupakan suatu pengelompokan dari sebagaian atau seluruh elemen dari suatu himpunan tanpa memperhatikan urutan susunan pemilihannya. Cara untuk menentukan banyaknya kombinasi yaitu dengan menggunakan rumus di bawah ini:

Sebagai contoh:
Kombinasi dari 2 elemen dari 3 huruf a,b,c yaitu ab, ac, bc . Sementara ba, ca, cb tidak termasuk ke dalam hitungan sebab dalam kombinasi ab=ba, ac=ca, bc=cb. Banyak kombinasi yaitu …
![]()
Binom Newton
Binom Newton berkaitan dengan bentuk dari (a + b)2 a. Di mana suku ke-r dari bentuk tersebut yaitu:
Suku ke – r = nCr-1 × an-r+1 × br-1
Sebagai ilustrasi:
koefisien dari x27 dari (x2 +2x)15 adalah:
nCr-1xan-r+1xbr-1 = 15 Cr-1x(x2)15-r+1x(2x)r-1
=15 Cr-1x(x30-2r+2)x(2x)r-1
Supaya x berpangkat 27 maka dibikin:
27 = (30 – 2r – 2) + (r – 1) → r = 4
Sehingga:
- suku ke – 4 = 15Cr-1x(x30-2r+2)x(2x)r-1 = 15C3x(x30-8+2)x(2x)4-1
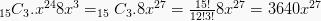 .
.- Koefisiennya: 3640
Peluang Suatu Kejadian
Nilai-nilai peluang yang didapatkan berkisar antara 0 hingga dengan 1. Untuk masing-masing kejadian A, batas-batas dari nilai P(A) secara matematis dapat kita tuliskan seperti berikut ini:
0 ≤ P (A) ≤ 1 dengan P(A) merupakan peluang suatu kejadian A
Apabila P(A) = 0, maka kejadian A merupakan kejadian yang mustahil, maka peluangnya tak lain adalah 0
Sebagai contoh:
Matahari yang terbit di sebelah selatan merupakan suatu kejadian yang mustahil, sehingga peluangnya tak lain adalah = 0
Apabila P(A) = 1, maka kejadian A merupakan kejadian pasti
Sebagai contoh:
Makhluk yang bernyawa pasti nanti akan mati hal itu adalah suatu kejadian pasti, sehingga peluangnya adalah = 1
Terdapat juga peluang kejadian yang bernilai antara 0 dan 1, yang artinya kejadian tersebut mungkin terjadi.
Sebagai contoh peluang seorang murid untuk menjadi juara kelas. Apabila L adalah kejadian komplemen dari kejadian A maka peluang dari kejadian L merpakan 1- peluang kejadian A.
Secara matematis dapat ditulis sebagai:
P (L) = 1 – P(A) atau bisa juga P(L) + P(A) = 1
Sebagai contoh:
Apabila peluang turun hujan pada hari ini adalah = 0,6 maka peluang untuk tidak turun hujan pada hari ini adalah = 1 – P (hujan)
= 1 – 0,6
= 0,4
1. Frekuensi Harapan
Frekuensi harapan dalah sebuah kejadian merupakan suatu harapan banyaknya muncul pada sebuah kejadian dari sejumlah percobaan yang dilakukan.
Secara matematis dapat dituliskan seperti di bawah ini:
Frekuensi harapan = P(A) x banyak percobaan
Sebagai contoh:
Dalam percobaan pengetosan sebuah dadu yang dilakukan sebanyak 60 kali, maka :
Peluang muncul mata 2 adalah = 1/6
Frekuensi harapan muncul mata 2 adalah = P (mata 2) x banyak percoban
= 1/6 x 60
= 10 kali
2. Kejadian Majemuk
Kejadian majemuk merupakan dua atau lebih kejadian yang dioperasikan sehingga akan membentuk sebuah kejadian yang baru.
Sebuah kejadian K serta kejadian komplemen berupa K’ memenuhi persamaan:
P(K) + P(K’) = 1 atau P(K’) = 1 – P(K)
Penjumlahan Peluang
1. Kejadian Saling Lepas
Terdapat buah kejadian A dan B bisa disebut sebagai kejadian saling lepas jika tidak ada satupun elemen yang terjadi pada kejadian A yang sama dengan elemen yang berlangsung pada kejadian B.
Sehingga peluang salah satu A atau B mungkin terjadi, rumus untuk kejadian saling lepas yaitu:
P(A u B) = P(A) + P(B)
2. Kejadian Tidak Saling Lepas
Maksutdnya yaitu elemen A yang sama dengan elemen B, rumus matematikanya bisa kita tuliskan seperti di bawah ini:
P(A u B) = P(A) + P(B) – P(A n B)
3. Kejadian Bersyarat
Kejadian bersyarat bisa berlangsung jika kejadian A bisa mempengaruhi munculnya kejadian B maupun sebaliknya. Maka dari itu rumusnya bisa kita tuliskan seperti di bawah ini:
P(A n B) = P(A) x P(B/A)
atau
P(A n B) = P(B) x P(A/B)
Sebab kejadiannya itu saling berpengaruh, maka juga bisa menggunakan rumus:
P(A n B) = P(A) x P(B)
Contoh Soal dan Pembahasan Kaidah Pencacahan
Setelah memahami materi mengenai kaidah pencacahan, kini saatnya kita belajar menyelesaikannya dalam beberapa soal.
Berikut akan kami berikan contoh soal sekaligus pembahasan mengenai kaidah pencacahan, mulai dari peluang, hingga permutasi dan yang lainnnya.
Soal 1.
Terdapat 3 orang anak yang akan duduk bersama di satu bangku yang memanjang. Ada berapakah cara mereka untuk duduk bersama pada bangku tersebut?
Jawab:
Ketiga anak akan duduk bersama, maka kita akan menggunakan rumus permutasi P(3,3)
P(3,3) = 3 = 2x2x1 = 6
Sehingga ketiga anak tersebut dapat duduk bersama dengan menggunakan 6 cara.
Soal 2.
Ada berapakan cara untuk menyusun dua huruf dari satu kata “HIDUP”?
Jawab:
Cara untuk menyusun 2 huruf dari 5 huruf, maka kita juga akan memakai rumus permutasi P(5,2)
P(5,2) = (5!)/(5-2) =(5x4x3!)/(3)! = 5×4 =20
Sehingga cara menyusun dua huruf dari satu kata HIDUP ada sebanyak 20 cara.
Soal 3.
Suatu huruf dipilih secara abstrak dari huruf-huruf pada tulisan ” JURAGAN”. Maka tentukanlah peluang terpilihnya huruf A!
Jawab:
Banyak kejadian yang dimaksud adalah = 2 sebab huruf A terdapat 2 di dalam kata “JURAGAN”
Banyak kejadian yang mungkin adalah = 7 sebab jumlah huruf ada 7
Sehingga P (huruf A) adalah = 2/7
Soal 4.
Terdapat sebuah kotak yang berisi 5 bola merah serta 4 bola hijau di dalamnya. Jika dua buah bola diambil satu persatu tanpa adanya pengembalian, tentukanlah peluang bola yang terambil merupakan bola merah pada pengambilan pertama serta bola hijau pada pengambilan kedua!
Jawab:
Pada pengambilan bola pertama tersedia sebanyak 5 bola yang berwarna merah dari 9 bola yang ada.
Sehingga P(M) = 5/9
Pada pengambilan kedua terdapat 4 bola hijau dari 8 bola yang tersisa (dengan syarat bola merah sudah terambil).
Sehingga P(H/M) = 4/8
Sebab kejadiannya saling berpengaruh, maka memakai rumus:
P(M n H) = P(M) x P(H/M)
P(M n H) = 5/9 x 4/8 = 5/18
Soal 5.
Pada percobaan melemper dua buah dadu, tentukan peluang munculnya angka genap pada dadu pertama serta angka ganjil prima pada dadu kedua!
Jawab:
Misal A = kejadian munculnya mata dadu genap di dadu pertama = {2,4,6} sehingga P(A) = 3/6
Misal B = kejadian munculnya mata dadu ganjil prima di dadu kedua = {3,5} maka P(B) = 2/6
Sebab kejadian A tidak akan berpengaruh pada kejadian B maka memakai rumus:
P(A n B) = P(A) x P(B)
P(A n B) = 3/6 x 2/6 = 1/6
Demikianlah ulasan singkat mengenai Kaidah Pencacahan yang dapat kami sampaikan. Semoga ulasan di atas mengenai Kaidah Pencacahan dapat kalian jadikan sebagai bahan belajar kalian.
The post Kaidah Pencacahan appeared first on Tuliskan.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment