Uraian: Permutasi dan Kombinasi (Lengkap)

Permutasi dan Kombinasi - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Permutasi dan Kombinasi?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Permutasi dan Kombinasi ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Permutasi dan Kombinasi

Setelah sebelumnya kita membahas mengenai rumus peluang, kini saatnya kita bahas mengenai permutasi dan kombinasi  yang ada di dalam materi peluang.

Dalam materi permutasi ini merupakan salah satu materi peluang yang membahas mengenai penyusunan k objek dari n objek yang tersedia dengan cara memperhatikan urutannya.

Sementara kombinasi berfungsi untuk menentukan penyusunan k objek dari n objek yang tersedia tanpa memperhatikan letak urutannya. 

Yuk langsung aja simak baik-baik ulasan berikut ini.

Permutasi

Materi pertama yang akan kita bahas pada artikel ini adalah permutasi. Permutasi mempelajari mengenai menyusun k objek dari n objek dengan cara memperhatikan urutan.

Ada tiga contoh permutasi yang sering timbul antara lain: permutasi dari unsur-unsur yang berbeda, permutasi dengan beberapa unsur yang sama, serta permutasi siklis. Selengkapnya simak baik-baik ulasan berikut ini.

Macam dan Formula atau Rumus Permutasi

1. Permutasi dari n elemen, masing-masing permutasi terdiri atas n elemen

Apabila terdapat unsur yang berbeda dan diambil n unsur, maka banyaknya susunan atau permutasi yang berbeda dari n unsur tersebut merupakan P_(n,n) = n! atau _nP_n = n!

Sebagai contoh:

Untuk menyambut suatu pertemuan delegasi negara yang dihadiri oleh lima negara. Panitia kemudian akan memasang kelima bendera yang merupakan bendera dari lima negara yang hadir.

Banyak cara untuk panitia menyusun kelima bendera tersebut yaitu?

Jawab:

Dari kelima bendera yang ada, berarti kita peroleh n = 5, sehingga banyak susunan bendera yang mungkin yakni:

5! = 5.4.3.2.1 = 120 cara.

2. Permutasi n elemen, masing-masing permutasi terdiri atas r unsur dari n elemen dengan r ≤ n

Untuk semua bilangan positif n dan r, dengan r≤n, banyaknya permutasi dari n objek yang diambil r objek pada satu waktu adalah:

Catatan:
Syarat: urutan harus diperhatikan.

Sebagai contoh:

Banyak cara untuk memilih seorang ketua, sekertaris dan juga bendahara dari 8 siswa yang tersedia yaitu…

Jawab:

Banyak siswa, n = 8

Ketua, sekretaris serta bendahara (banyak pilihan objek), r = 3

Sehingga:

3. Permutasi dari n unsur yang mengandung p.q dan r unsur yang sama

Keterangan:

n    = menunjukan banyaknya elemen seluruhnya

k₁  = menunjukan banyaknya elemen kelompok 1 yang sama

k₂  = menunjukan banyaknya elemen kelompok 2 yang sama

…

k_t   = menunjukan banyaknya elemen kelompok kt yang sama

t = 1,2,3,…

Sebagai cottoh:

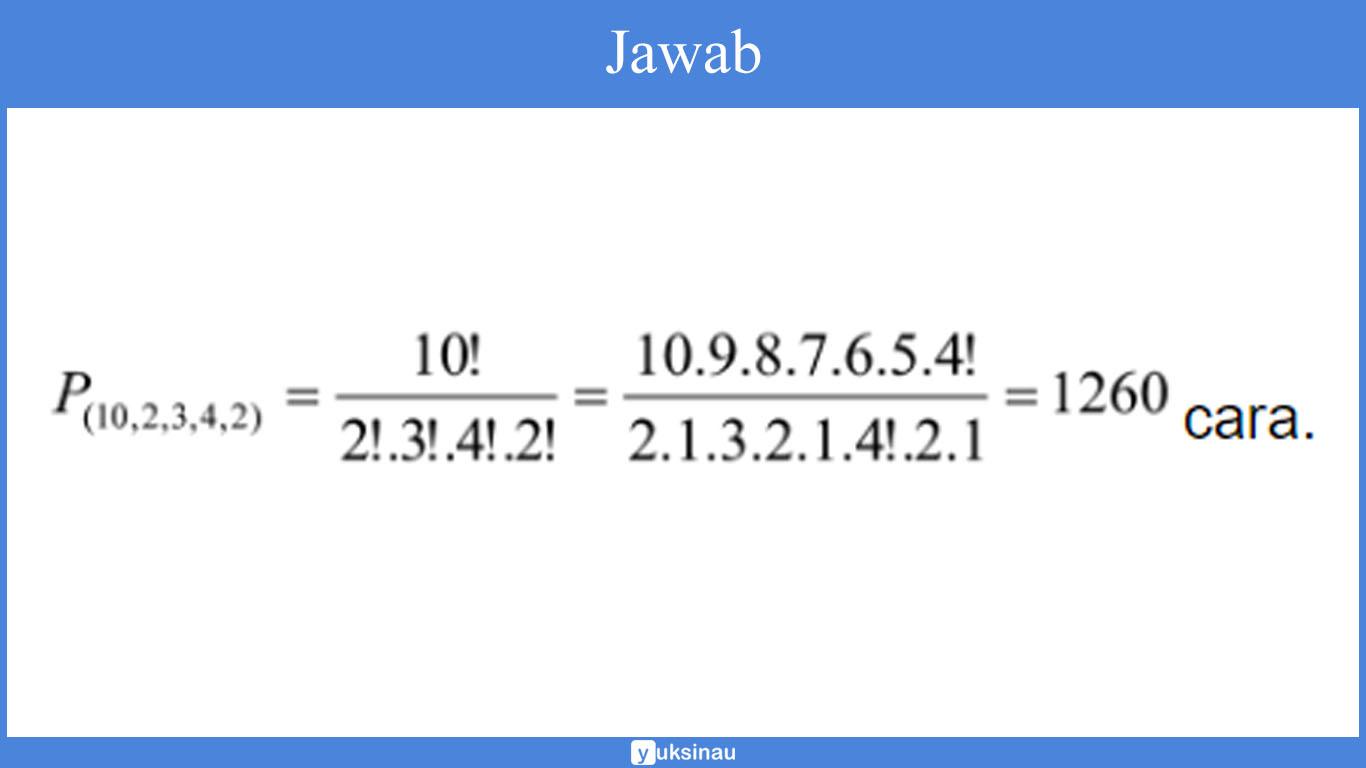
Banyaknya cara penyusunan untuk kata ”BASSABASSI” yaitu…

Jawab:

Dari kata ”BASSABASSI”, banyak huruf adalah (n) = 10

k₁ = huruf B = 2

k₂ = huruf A = 3

k₃ = huruf S = 4

k₄ = huruf I = 1

4. Permutasi Siklis

Permutasi siklis merupakan suatu permutasi melingkar (urutan melingkar).

_nP_siklis = (n-1)!

Sebagai contoh:

Dari 5 orang anggota keluarga akan segera duduk mengelilingi satu meja bundar, banyaknya cara penyusunan yang bisa dibikin dari 5 orang tersebut yaitu…

Jawab:

Banyak orang (n) = 5, sehingga:

₅P_siklis = (5 – 1)! = 4! = 4.3.2.1 = 24 cara.

5. Permutasi berulang dari n unsur, tipe permutasi terdiri dari k unsur

P_n = n^k

Contoh:

Banyak susunan dari 3 bilangan angka-angka 1, 2, 3, 4, 5 dan 6 yaitu…

Jawab:

• Banyaknya susunan 3 bilangan, yang artinya bilangan ratusan, k = 3
• Banyak angka yang akan disusun adalah n = 6
• Banyak susunan 3 bilangan dari angka 1, 2, 3, 4, 5, serta 6, sehingga:

P₆ = 6³ = 216 susunan.

Kombinasi

Sepeti yang telah dijelaskan di atas, kombinasi merupakan suatu susunan yang tidak memperhatikan urutan.

Sebagai contoh permasalahan yang memakai kombinasi merupakan mengetahui banyaknya cara untuk mengambil 3 bola dari 5 bola merah serta 2 bola hijau yang tersedia dalam suatu kotak.

Di dalam kotak tersebut berisi beberapa warna bola yang berbeda yaitu bola merah, merah, dan kuning.

Cara pengambilan lain yang mungkin merupakan merah, kuning merah, dan yang lainnya.

Sebagai contoh bola warna merah itu kita beri nomor satu hingga dengan lima serta bola kuning juga diberi nomor satu sampai dua.

Cara pengambilan bola pertama yang berwarna merah dengan nomor dua akan sama dengan terambilnya bola yang berwarna merah dengan nomor satu.

Begitu juga dengan bola dengan nomor dan juga warna yang berbeda. Masih bingung? Tenang, coba perhatikan tabel di bawah ini.

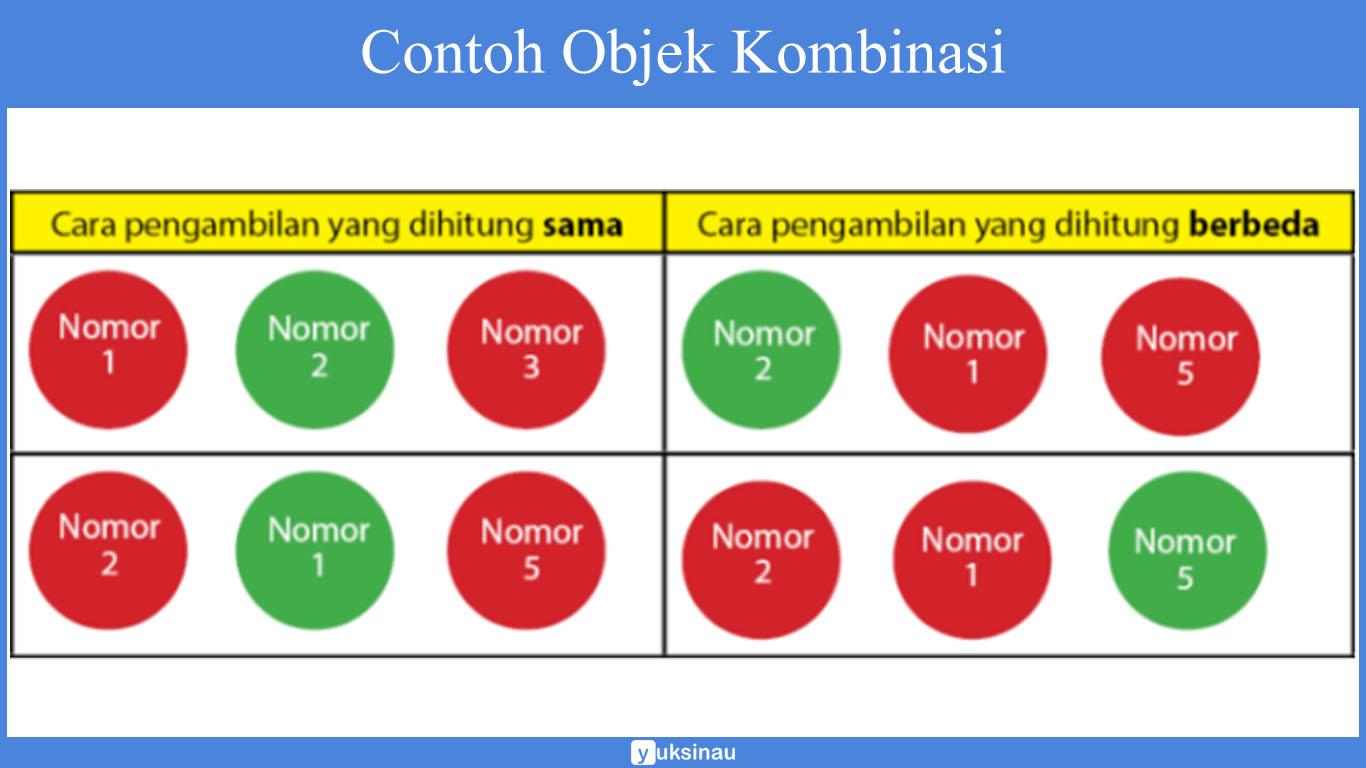
Mengetahui jumlah banyaknya cara untuk menyusun k objek dari n objek yang tersedia maka kita memerlukan banyak waktu dan tentu tidak efektif.

Di dalam ilmu peluang, terdapat suatu rumus yang bisa kita pakai untuk menyusun k objek dari n objek yang tersedia.

Rumus tersebut merupakan rumus dalam kombinasi. Banyaknya kombinasi k unsur yang diambil dari n unsur yang tersedia akan dinyatakan dalam rumus kombinasi seperti di bawah ini:

Perbedaan Permasalah Permutasi dan Kombinasi

Setelah mengetahui apa itu permutasi dan kombinasi, hal yang tak kalah penting untuk dikethui adalah membedakan permasalahan mana yang termasuk ke dalam permutasi ataupun kombinasi.

Permasalahan yang sering muncul biasanya berwujud soal cerita.

Serta kita dituntut supaya dapat membedakan masalah itu termasuk dalam permutasi atau kombinasi. Sehingga kita tidak akan mengalami kesalahan dalam pemakian rumus untuk menyelesaikan masalah tersebut.

Perhatikan dua contoh kasus di bawah ini:

Kasus pertama: permasalahan permutasi

Susunan panitia yang terdiri atas ketua, wakil ketua, sekretaris, serta bendahara akan dibentuk untuk mensukseskan suatu acara. Susunan panitia itu kemudian akan memilih dari 10 orang terpilih berdasarkan kriteria yang sudah ditetapkan. Jadi, berapakan banyaknya cara untuk menyusun panitia hingga bisa terbentuk?

Kasus ke dua: permasalahan kombinasi

Enam buku akan dipilih dari lima buku Matematika, tiga buku Fisika, serta empat buku Kimia untuk akan disumbangkan ke sekolah untuk para anak jalanan.

Hitunglah berapa banyaknya cara yang bisa dilakukan untuk memilih keenam buku itu?

Dalam kasus pertama, susunan urutan akan menjadi satu sisi yang perlu untuk diperhatikan. Kedudukan dari ketua untuk orang pertama tentu akan berbeda dengan kedudukan ketua yang ditempati oleh orang ke tiga.

Begitu pula untuk kududukan di posisi lainnya.

Sementara di contoh kasus yang kedua, pemilihan buku pada urutan pertama dan kedua contohnya diambil buku Matematika pertama serta buku Matematika ke dua, dimana keduanya adalah buku Matematika.

Sehingga, urutan pada kasus kedua tidak dipehatikan.

Intinya, rumus permutasi dipakai untuk suatu kasus atau permasalahan yang memperhatikan urutan. Sementara untuk kombinasi dipakai untuk menyelesaikan permasalahan yang tidak memperhatikan urutan.

Contoh Soal dan Pembahasan

Soal 1.

Terdapat 3 orang anak yang akan duduk bersama di satu bangku yang memanjang. Ada berapakah cara mereka untuk duduk bersama pada bangku tersebut?

Jawab:

Ketiga anak akan duduk bersama, maka kita akan menggunakan rumus permutasi P(3,3)

P(3,3) = 3 = 2x2x1 = 6

Sehingga ketiga anak tersebut dapat duduk bersama dengan menggunakan 6 cara.

Soal 2.

Ada berapakan cara untuk menyusun dua huruf dari satu kata “HIDUP”?

Jawab:

Cara untuk menyusun 2 huruf dari 5 huruf, maka kita juga akan memakai rumus permutasi P(5,2)

P(5,2) = (5!)/(5-2) =(5x4x3!)/(3)! = 5×4 =20

Sehingga cara menyusun dua huruf dari satu kata HIDUP ada sebanyak 20 cara.

Soal 3.

Dalam suatu kelas terdiri dari 7 murid perempuan dan juga 3 murid laki-laki. Dari kelas itu kemudian akan dipilih 3 orang murid secara acak. Maka peluang bahwa yang terpilih ketiga-tiganya perempuan yaitu …

A. 2/91
B. 1/12
C. 1/3
D. 1/5
E. 3/5

Jawab:

Banyaknya cara untuk memilih 3 murid dari 10 murid secara acak (contohnya dengan variabel n):

Dalam permasalahan ini, urutan tidak menjadi hal yang perlu diperhatikan, sehingga rumus yang digunakan adalah kombinasi.

Banyaknya cara untuk memilih 3 murid dari 10 murid secara acak (misalkan dengan variabel n):

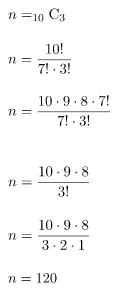
Banyaknya cara untuk memilih 3 murid perempuan dari 7 murid perempuan (contohnya dengan variabel k):

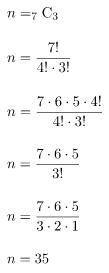
Peluang bahwa yang terpilih ketiga-tiganya perempuan adalah:

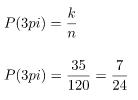
Jawabannya: A

Baca juga: Rumus Peluang

Demikianlah ulasan singkat mengenai Permutasi dan Kombinasi yang dapat kami sampaikan. Semoga ulasan di atas mengenai Permutasi dan Kombinasi dapat kalian jadikan sebagai bahan belajar kalian.

The post Permutasi dan Kombinasi appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Permutasi dan Kombinasi (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.