Uraian: Rumus Peluang (Lengkap)

Rumus Peluang - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Rumus Peluang?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Rumus Peluang ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Rumus Peluang

Tanpa kita sadari, konsep dari rumus peluang matematika banyak kita jumpai dalam kehidupan sehari-hari. Sebagai contoh uang logam atau koin.

Pastinya kita pernah dong, melihat uang yang berwujud logam atau koin ini. Dan dalam mata uang tersebut terdiri dari dua buah sisi.

Kita misalkan jika sisi pertama merupakan angka, sementaara untuk sisi kedua merupakan gambar.

Apabila uang logam tersebut kita lemparkan ke udara sebanyak satu kali. Berapa peluang dari munculnya angka?

Sementara apabila jika kita lemparkan sebanyak 2 kali 3 kali bahkan 10 kali maka berapa peluang munculnya angka?

Nah, konsep yang demikianlah yang disebut sebagai peluang. Untuk mengetahui apa itu peluang lebih lanjut mari kita pelajari bersama-sama mengenai materi rumus peluang. Simak baik-baik artikel ini sampai selesai ya.

Pengertian peluang

Peluang dapat didefiniskan sebagai suatu cara yang dilakukan guna mengetahui kemungkinan terjadinya suatu peristiwa.

Dalam setiap permasalahan yang ada ketidakpastian yang dikarenakan dari sebuah tindakan yang terkadang berakibat lain.

Sebagai contoh: pada uraian di atas disebutkan bahwa sebuah mata uang logam yang dilemparkan ke udara akibatnya bisa memunculkan sisi gambar (G) atau sisi angka (A). Sehingga sisi yang akan muncul tidak bisa kita tentukan secara pasti.

Akibat dari melemparkan sebuah mata uang logam merupakan salah satu dari dua kejadian yang bisa terjadi yakni munculnya sisi G atau A.

Kegiatan daru melemparkan mata uang logam tersebut disebut sebagai sebuah tindakan acak. Tindakan itu bisa kita ulang beberapa kali serta rangkaian tindakan tersebut disebut sebagai percobaan.

Tindakan dari satu kali aktifitas juga bisa dinyatakan sebagai suatu percobaan.

Rumus Peluang Matematika

Percobaan untuk melemparkan mata uang logam hasilnya bisa memunculkan G atau A.

Jika percobaan yang kita lakukan dengan cara melempar 10 kali serta memunculkan G sebanyak 4 kali maka frekuensi relatif munculnya G yaitu 4/10.

Namun, apabila percobaan yang kita lakukan sebanyak 10 kali lagi serta hanya memunculkan G sebanyak 3 kali sehingga dalam 20 kali percobaam G muncul sebanyak 7 kali maka frekuensi relatif muncul G pada 20 percobaan ialah 7/20.

Frekuensi Relatif

Frekuensi adalah suatu perbandingan antara banyaknya percobaan yang kita lakukan dengan banyaknya kejadian yang diamati.

Dari suatu percobaan dengan melemparkan mata uang logam tadi maka dapat kita ketahui frekuensi relatif bisa dirumuskan seperti di bawah ini:

Contoh soal:

Pada percobaan melempar mata uang logam dilakukan sebanyak 100 kali. Ternyata permukaan gambar (g) muncul sebanyak 30 kali.

Sehingga dapat kita katakan frekuensi relatif muncul gambar pada soal di atas adalah = 30/100 = 3/10

Peluang

Contoh soal:

Pada percobaan mengetos atau melempar undi pada sebuah mata uang logam maka:

Peluang muncul angka adalah = 1/2

1 merupakan banyaknya permukaan angka pada mata uang.

2 merupakan adanya dua kemungkinan yakni muncul angka atau gambar.

Ruang Sampel

Ruang sampel adalah suatu himpunan dari keseluruhan kejadian (hasil) percobaan yang mungkin terjadi. Ruang sampel dilambangkan dengan huruf S.

Contoh:

• Ruang sampel pada pengetosan di sebuah dadu yaitu S = (1, 2, 3, 4, 5, 6)
• Ruang sampel pada pengetosan pada sebuah mata uang logam yaitu S = (A, G)

Menentukan Ruang Sampel

Ruang sampel hasil dari melempar dua mata uang bisa kita tentukan dengan cara memakai tabel (daftar) seperti yang ada di bawah ini:

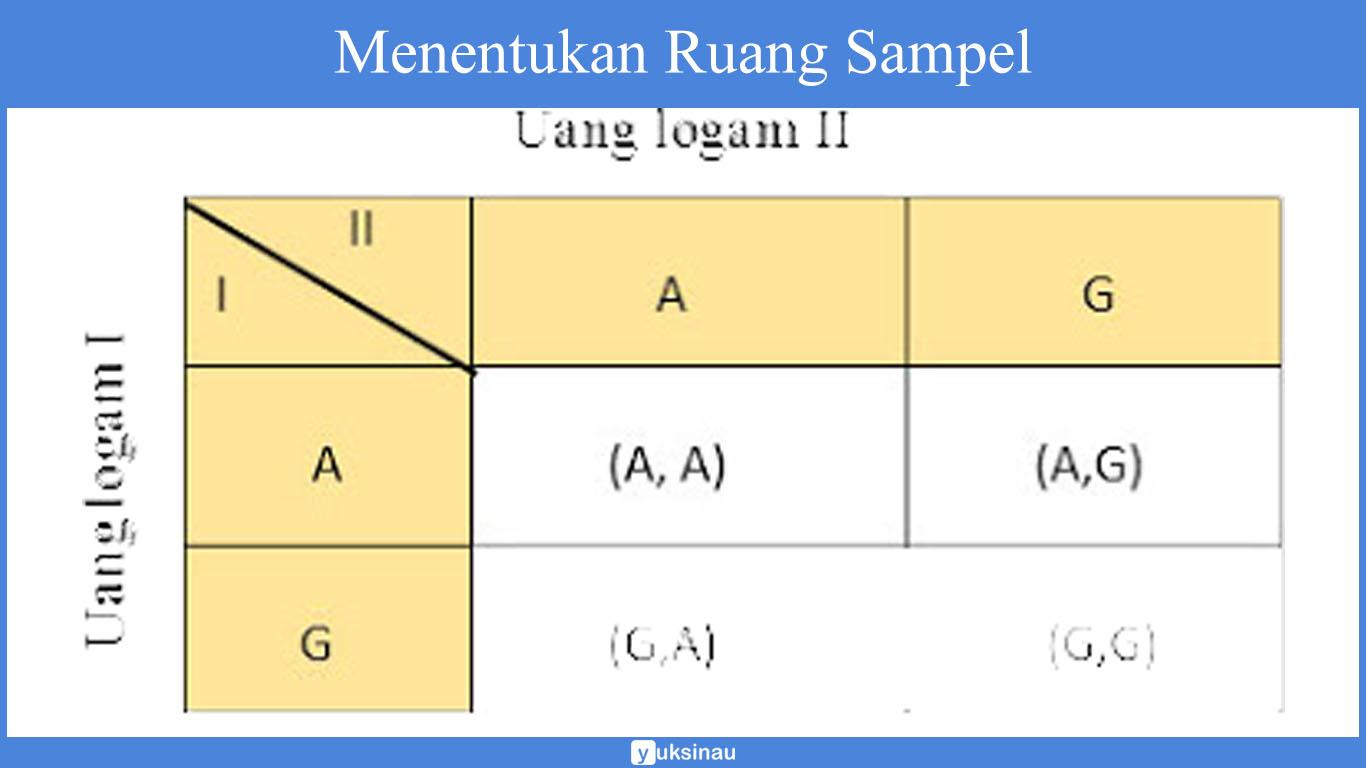
Ruang sampelnya yakni: S = {(A,A), (A,G), (G,A), (G,G)}
Kejadian A1 yang memuat dua gambar adalah = (G,G)
Kejadian A2 yang tidak memuat gambar adalah = (A,A)

Titik Sampel

Titik sampel merupakan anggota-anggota yang berasal dari ruang sampel.

Sebagai contoh:

Ruang sampel dari S =  ((A,A), (A,G), (G,A), (G,G))

Titik sampelnya antara lain: ((A,A), (A,G), (G,A), (G,G))

Peluang Kejadian A atau P(A)

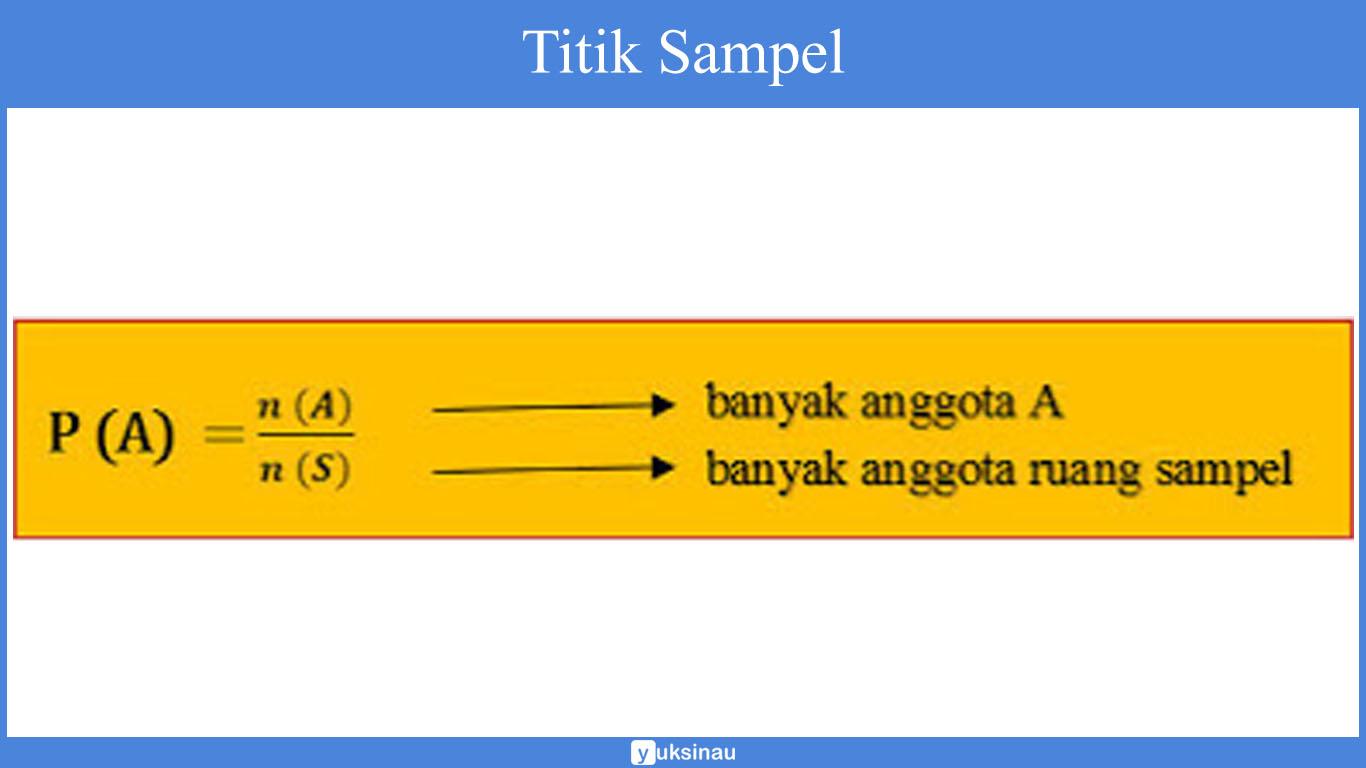
Peluang kejadian bisa kita tentukan dengan menggunakan cara seperti di bawah ini:

S = {1,2,3,4,5,6} maka nilainya n(S) = 6

A = {2,3,5} maka n(A) = 3

Dari penjelasan di atas menerangkan bahwa apbila masing-masing titik sampel dari anggota ruang sampel S mempunyai peluang yang sama. Maka peluang kejadian A yang jumlah anggotanya dinyatakan dalam n(A) maka bisa dinyatakan dengan menggunakan rumus di bawah ini:

Nilai Peluang

Nilai-nilai peluang yang didapatkan berkisar antara 0 hingga dengan 1. Untuk masing-masing kejadian A, batas-batas dari nilai P(A) secara matematis dapat kita tuliskan seperti berikut ini:

0 ≤ P (A)  ≤ 1 dengan P(A) merupakan peluang suatu kejadian A

Apabila P(A) = 0, maka kejadian A merupakan kejadian yang mustahil, maka peluangnya tak lain adalah 0

Sebagai contoh:

Matahari yang terbit di sebelah selatan merupakan suatu kejadian yang mustahil, sehingga peluangnya tak lain adalah = 0

Apabila P(A) = 1, maka kejadian A merupakan kejadian pasti

Sebagai contoh:

Makhluk yang bernyawa pasti nanti akan mati hal itu adalah suatu kejadian pasti, sehingga peluangnya adalah = 1

Terdapat juga peluang kejadian yang bernilai antara 0 dan 1, yang artinya kejadian tersebut mungkin terjadi.

Sebagai contoh peluang seorang murid untuk menjadi juara kelas. Apabila L adalah kejadian komplemen dari kejadian A maka peluang dari kejadian L merpakan 1- peluang kejadian A.

Secara matematis dapat ditulis sebagai:

P (L)  = 1 – P(A) atau bisa juga P(L) + P(A) = 1

Sebagai contoh:

Apabila peluang turun hujan pada hari ini adalah = 0,6 maka peluang untuk tidak turun hujan pada hari ini adalah = 1 – P (hujan)
= 1 – 0,6
= 0,4

1. Frekuensi Harapan

Frekuensi harapan dalah sebuah kejadian merupakan suatu harapan banyaknya muncul pada sebuah kejadian dari sejumlah percobaan yang dilakukan.

Secara matematis dapat dituliskan seperti di bawah ini:

Frekuensi harapan = P(A) x banyak percobaan

Sebagai contoh:

Dalam percobaan pengetosan sebuah dadu yang dilakukan sebanyak 60 kali, maka :

Peluang muncul mata 2 adalah = 1/6

Frekuensi harapan muncul mata 2 adalah = P (mata 2) x banyak percoban
= 1/6 x 60
= 10 kali

2. Kejadian Majemuk

Kejadian majemuk merupakan dua atau lebih kejadian yang dioperasikan sehingga akan membentuk sebuah kejadian yang baru.

Sebuah kejadian K serta kejadian komplemen berupa K’ memenuhi persamaan:

P(K) + P(K’) = 1 atau P(K’) = 1 – P(K)

Penjumlahan Peluang

1. Kejadian Saling Lepas

Terdapat buah kejadian A dan B bisa disebut sebagai kejadian saling lepas jika tidak ada satupun elemen yang terjadi pada kejadian A yang sama dengan elemen yang berlangsung pada kejadian B.

Sehingga peluang salah satu A atau B mungkin terjadi, rumus untuk kejadian saling lepas yaitu:

P(A u B) = P(A) + P(B)

2. Kejadian Tidak Saling Lepas

Maksutdnya yaitu elemen A yang sama dengan elemen B, rumus matematikanya bisa kita tuliskan seperti di bawah ini:

P(A u B) = P(A) + P(B) – P(A n B)

3. Kejadian Bersyarat

Kejadian bersyarat bisa berlangsung jika kejadian A bisa mempengaruhi munculnya kejadian B maupun sebaliknya. Maka dari itu rumusnya bisa kita tuliskan seperti di bawah ini:

P(A n B) = P(A) x P(B/A)

atau

P(A n B) = P(B) x P(A/B)

Sebab  kejadiannya itu saling berpengaruh, maka juga bisa menggunakan rumus:

P(A n B) = P(A) x P(B)

Contoh Soal dan Pembahasan

Untuk lebih memahami materi rumus peluang matematika, simak beberapa contoh soal sekaligus pembahasannya yang akan kami sajikan di bawah ini:

Contoh Soal Peluang 1

Dalam percobaan melemparkan sebuah mata uang logam sebanyak 120 kali, ternyata banyaknya angka muncul sebanyak 50 kali.

Dari persoalan di atas, tentukanlah frekuensi relatif muncul angka dan frekuensi relatif muncul gambar!

Jawab:

Frekuensi relatif muncul angka = Banyak angka yang muncul atau Banyak percobaan
= 50/120
= 5/12

Frekuensi relatif muncul gambar = Banyak gambar yang muncul atau Banyak percobaan
= (120 – 50) / 120
= 70/120
= 7/12

Contoh Soal Peluang 2

Suatu huruf dipilih secara abstrak dari huruf-huruf pada tulisan ” JURAGAN”. Maka tentukanlah peluang terpilihnya huruf A!

Jawab:

Banyak kejadian yang dimaksud adalah = 2 sebab huruf A terdapat 2 di dalam kata “JURAGAN”

Banyak kejadian yang mungkin adalah = 7 sebab jumlah huruf ada 7

Sehingga P (huruf A) adalah = 2/7

Contoh Soal Peluang 3

Dua buah dadu ditos secara bersamaan. Maka tentukan peluang kejadian berikut ini !

a. Muncul dadu pertama bermata 4

b. Muncul mata dadu berjumlah 9

Jawab:

Kita bikin suatu ruang sampel atau tabel percobaan untuk mengetos dua dadu seperti berikut ini:

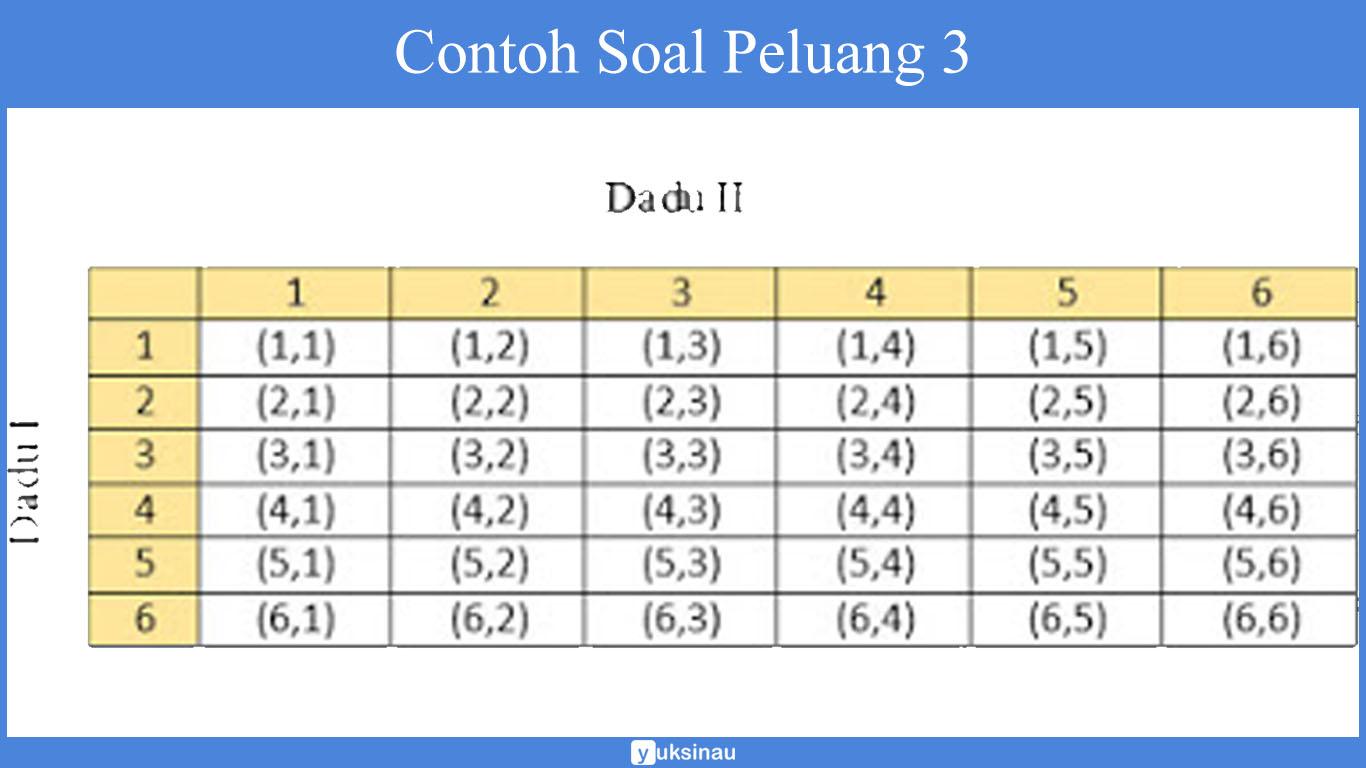
a. dadu pertama bermata 4, yang artinya dadu kedua bisa jadi bermata 1,2,3,4,5, atau 6. Dengan begitu, kejadian muncul dadu pertama bermata 4 yaitu:

M = {(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)}

Sehingga, P (dadu I bermata 4) = n(M)/n(S) = 6/36 = 1/6

b. Kejadian muncul mata dadu berjumlah 9 yaitu:

N = {(3,6), (4,5), (5,4), (6,3)}

Sehingga, P (jumlah 9) = n(N)/n(S) = 4/36 = 1/9

Contoh Soal Kejadian Saling Bebas 4.

Pada percobaan melemper dua buah dadu, tentukan peluang munculnya angka genap pada dadu pertama serta angka ganjil prima pada dadu kedua!

Jawab:

Misal A = kejadian munculnya mata dadu genap di dadu pertama = {2,4,6} sehingga P(A) = 3/6

Misal B = kejadian munculnya mata dadu ganjil prima di dadu kedua = {3,5} maka P(B) = 2/6

Sebab kejadian A tidak akan berpengaruh pada kejadian B maka memakai rumus:

P(A n B) = P(A) x P(B)

P(A n B) = 3/6 x 2/6 = 1/6

Contoh Soal Kejadian Bersyarat 5.

Terdapat sebuah kotak yang berisi 5 bola merah serta 4 bola hijau di dalamnya. Jika dua buah bola diambil satu persatu tanpa adanya pengembalian, tentukanlah peluang bola yang terambil merupakan bola merah pada pengambilan pertama serta bola hijau pada pengambilan kedua!

Jawab:

Pada pengambilan bola pertama tersedia sebanyak 5 bola yang berwarna merah dari 9 bola yang ada.

Sehingga P(M) = 5/9

Pada pengambilan kedua terdapat 4 bola hijau dari 8 bola yang tersisa (dengan syarat bola merah sudah terambil).

Sehingga P(H/M) = 4/8

Sebab kejadiannya saling berpengaruh, maka memakai rumus:

P(M n H) = P(M) x P(H/M)

P(M n H) = 5/9 x 4/8 = 5/18

Baca juga: Integral Tak Tentu

Demikianlah ulasan singkat mengenai Rumus Peluang yang dapat kami sampaikan. Semoga ulasan di atas mengenai Rumus Peluang dapat kalian jadikan sebagai bahan belajar kalian.

The post Rumus Peluang appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Rumus Peluang (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.