Uraian: Bangun Ruang Sisi Datar (Lengkap)
Namun tak ada salahnya sebelum membaca ulasan tentang Bangun Ruang Sisi Datar ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?
Pembahasan Lengkap Bangun Ruang Sisi Datar
Bangun ruang sisi datar merupakan suatu bangun tiga dimensi yang memiliki ruang/ volume/ isi dan juga sisi-sisi yang membatasinya.
Secara garis besar, bangun ruang bisa kita kategorikan menjadi dua kelompok, antara lain: bangun ruang sisi datar dan bangun ruang sisi lengkung.
Yang termasuk dalam bangun ruang sisi datar yaitu kubus, balok, prisma, dan limas. Sementara untuk bangun ruang sisi lengkung terdiri atas kerucut, tabung, dan bola.
Unsur Unsur Bangun Ruang
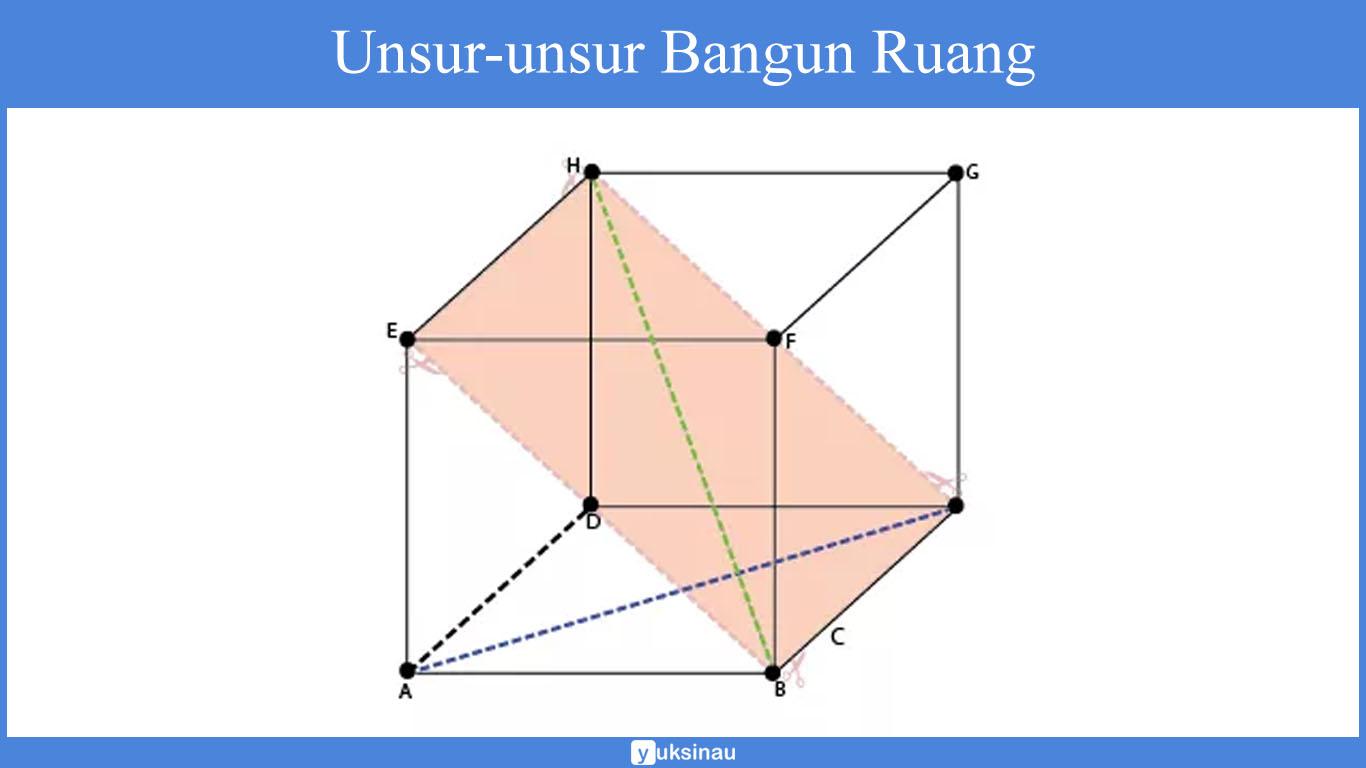
Keterangan:
ABCD: Sisi
AB: Rusuk
A: Titik Sudut
BH: Diagonal Ruang
AC: Diagonal Bidang
BCEH: Bidang Diagonal
Penjelasan:
- Bidang (Sisi) merupakan daerah yang membatasi bagian luar dengan bagian dalam dari sbeuah bangun ruang.
- Rusuk merupakan suatu perpotongan dua buah bidang yang berwujud garis.
- Titik sudut adalah perpotongan tiga buah rusuk.
- Diagonal bidang merupakan diagonal yang terletak dalam bidang bidang pembentuk bangun ruang atau pada sisi bangun ruang.
- Diagonal ruang merupakan garis yang melintasi ruang yang menghubungkan dua titik sudut yang tidak sebidang.
- Bidang diagonal merupakan suatu bidang yang melintasi ruang dalam bangun ruang.
| Bangun | Sisi | Rusuk | Titik Sudut | Diagonal Bidang | Diagonal Ruang | Bidang Diagonal |
| Kubus | 6 | 12 | 8 | 12 | 4 | 6 |
| Balok | 6 | 12 | 8 | 12 | 4 | 6 |
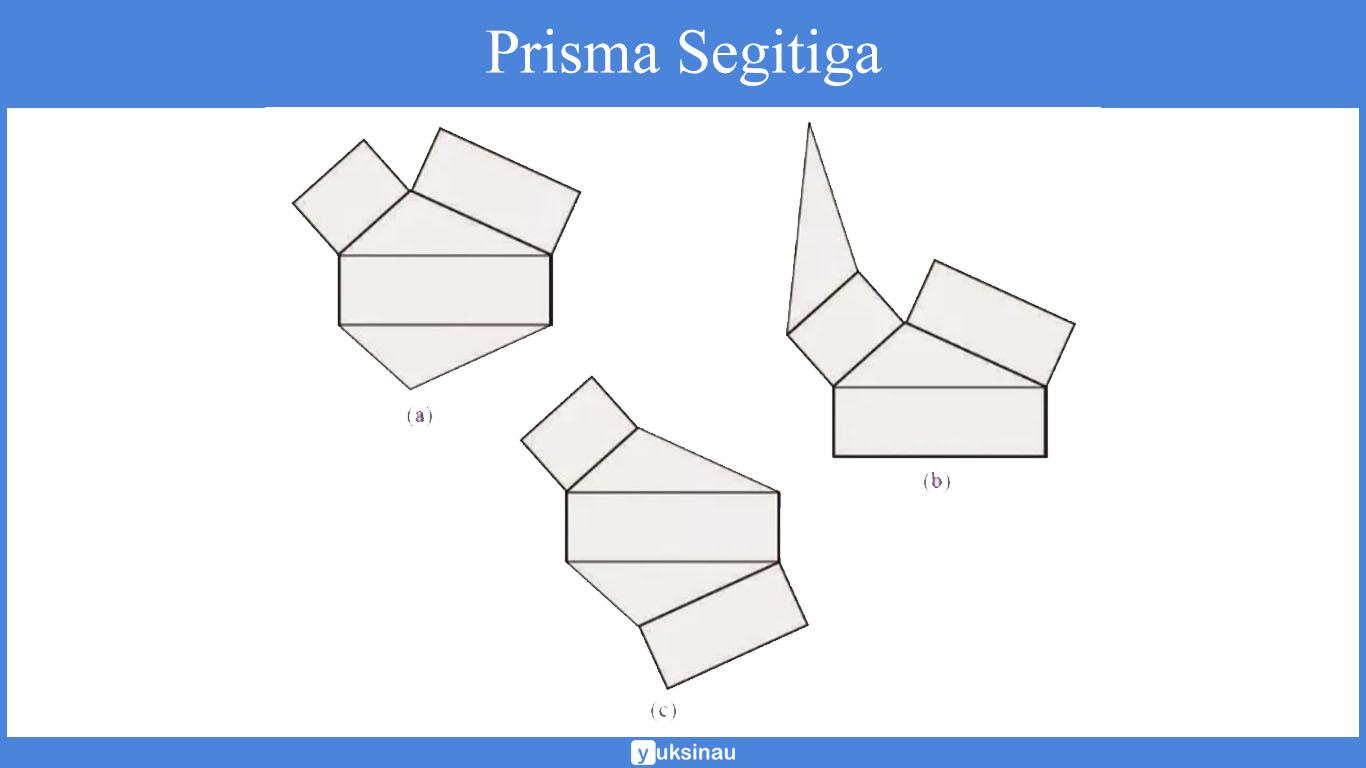
| Prisma Segitiga | 5 | 9 | 6 | 6 | – | – |
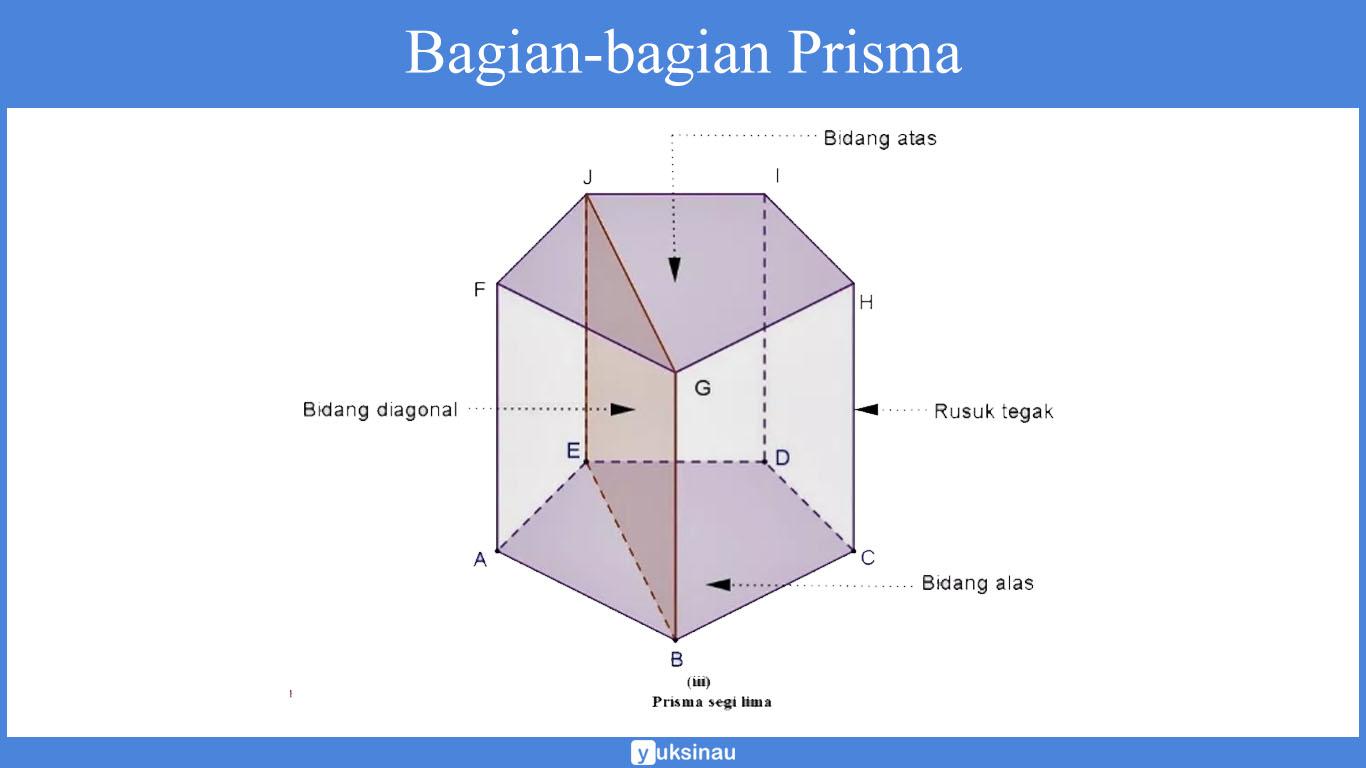
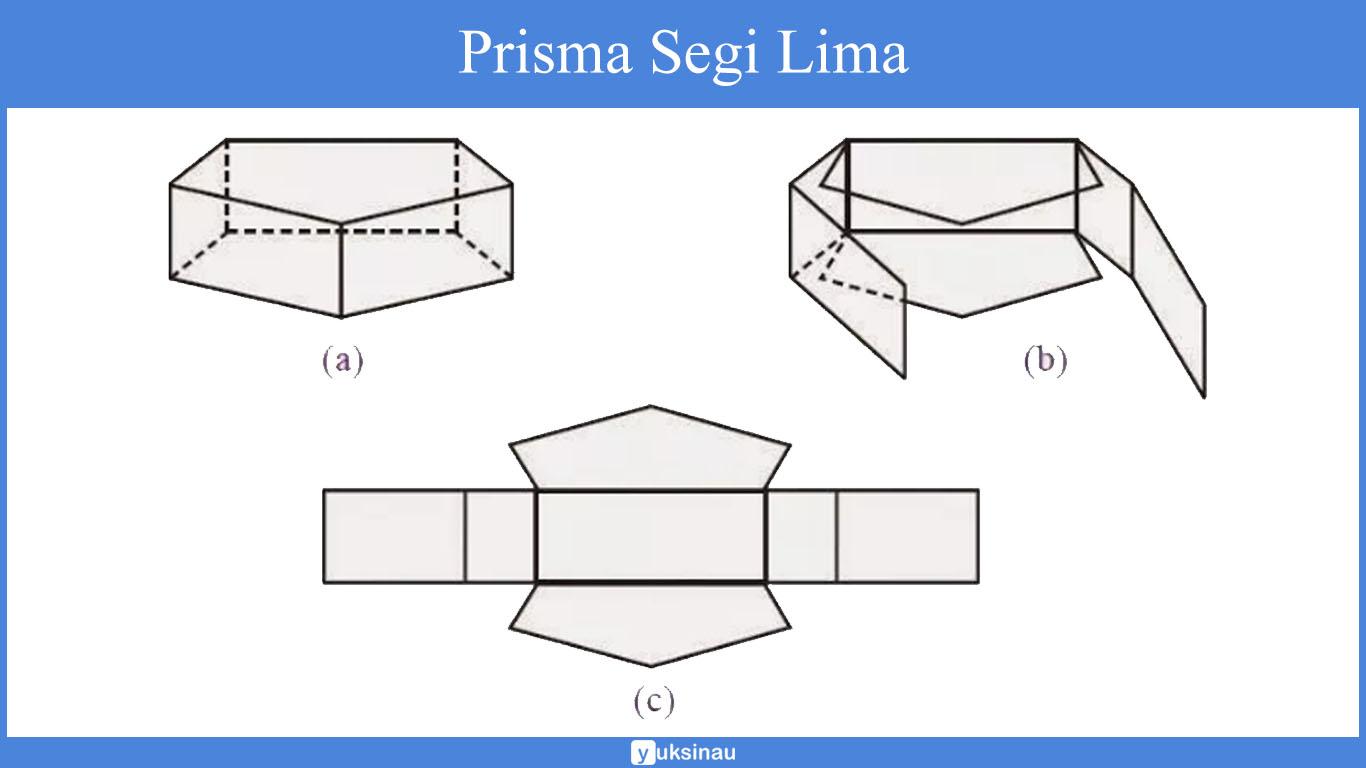
| Prisma Segi Lima | 7 | 15 | 10 | 20 | 10 | 5 |
| Prisma Segi-n | n+2 | 3n | 2n | n(n – 1) | n(n – 1) | ½ n(n – 3) |
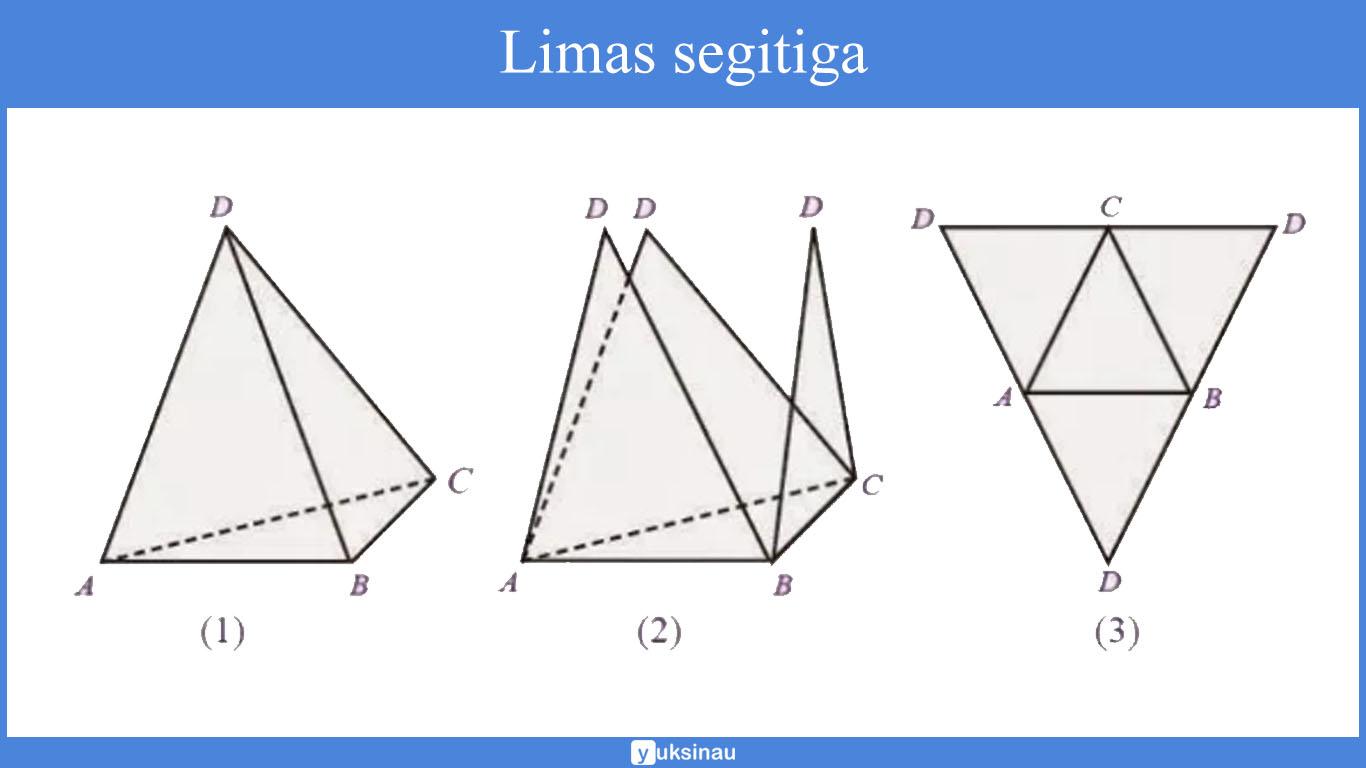
| Limas Segitiga | 4 | 6 | 4 | – | – | – |
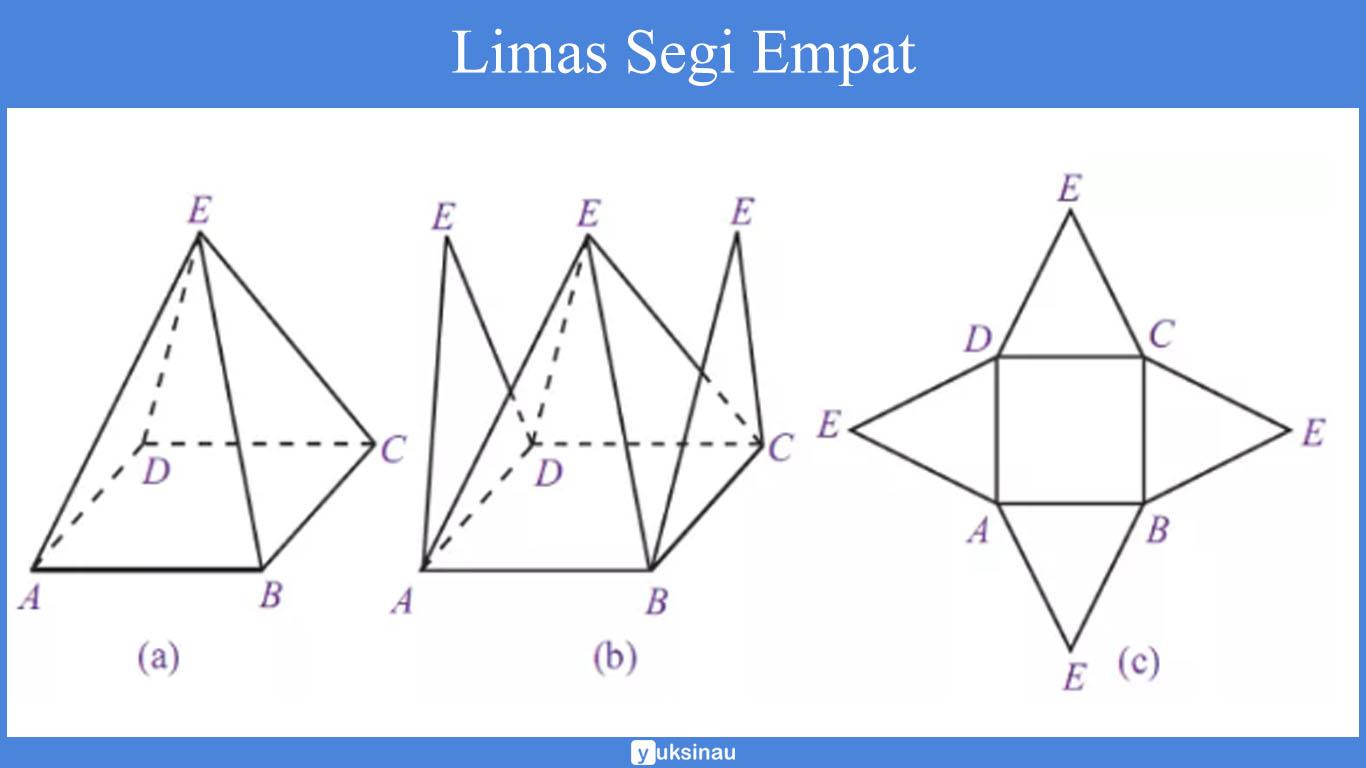
| Limas Segi Empat | 5 | 8 | 5 | 2 | – | – |
Macam Macam Bangun Ruang Sisi Datar
Bangun ruang sisi datar merupakan suatu bangun ruang di mana pada masing-masing sisinya tersusun dari bangun datar.
Apabila dalam suatu bangun ruang mempunyai satu saja sisi yang lengkung maka bangun tersebut tidak bisa dikatakan sebagai bangun ruang sisi datar.
Kubus
Pengertian Kubus
Kubus merupakan suatu bangun ruang tiga dimensi yang dibatasi oleh enam sisi serupa yang berwujud bujur sangkar.
Kubus juga dikenal dengan nama lain yaitu bidang enam beraturan. Kubus sebetulnya adalah bentuk khusus dari prisma segiempat, sebab tingginya sama dengan sisi alas.
Bagian-bagian Kubus
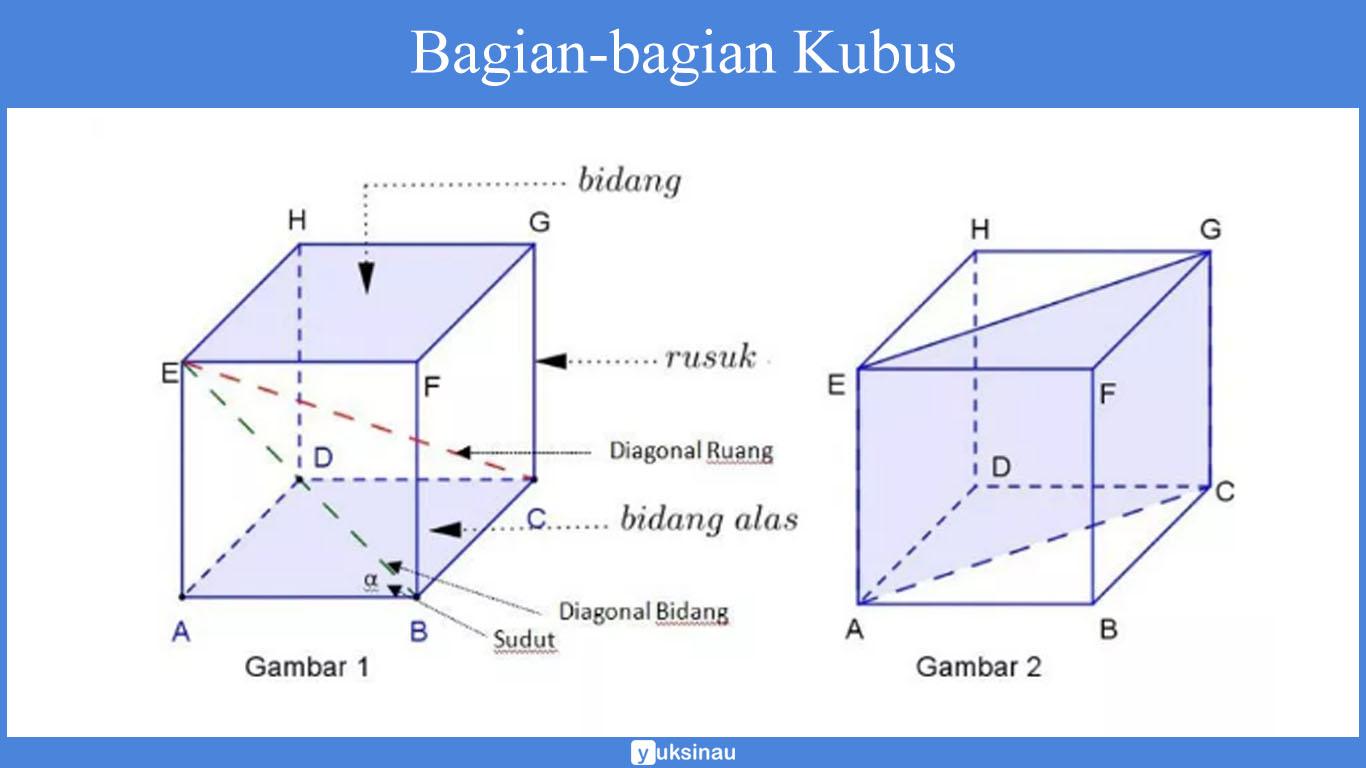
- Sisi kongruen ada sebanyak 6 buah yang terdiri atas:
- bidang alas kubus: ABCD
- bidang atas kubus: EFGH
- sisi tegak kubus: ABEF, CDGH, ADEH, dan BCFG.
- Rusuk sama panjang ada sebanyak 12 buah (AB = BC = CD = DA = EF = FG = GH = HE = AE = BF = CG = DH).
- Titik sudut berjumlah 8 titik (A, B, C, D, E, F, G, H).
- Diagonal bidang yang sama panjang sebanyak 6 buah (AC = BD = EG = FH = AF = BE = CH = DG = AH = DE = BG = CF).
- Diagonal ruang yang sama panjang sebanyak 4 buah (AG = BH = CE = DF).
- Bidang diagonal kongruen berjumlah 6 buah (ABGH, EFCD, BCHE, FGDA, BFHG, dan AEGC).
Sifat bangun Kubus
- Seluruh sisi kubus berbentuk persegi dengan mempunyai luas yang sama.
- Seluruh rusuk kubus memiliki panjang yang sama.
- Masing-masing diagonal bidang pada kubus mempunyai panjang yang sama.
Perhatikan ruas garis BG dan CF pada gambar di atas. Kedua garis tersebut adalah diagonal bidang kubus ABCD.EFGH yang mempunyai ukuran sama panjang. - Masing-masing diagonal ruang pada kubus memiliki panjang yang sama.
Dari kubus ABCD.EFGH pada gambar di atas , ada dua diagonal ruang, yakni HB dan DF di mana keduanya berukuran sama panjang. - Masing-masing bidang diagonal pada kubus berbentuk persegi panjang.
Perhatikan bidang diagonal ACGE pada gambar di atas.
Jaring Jaring Kubus
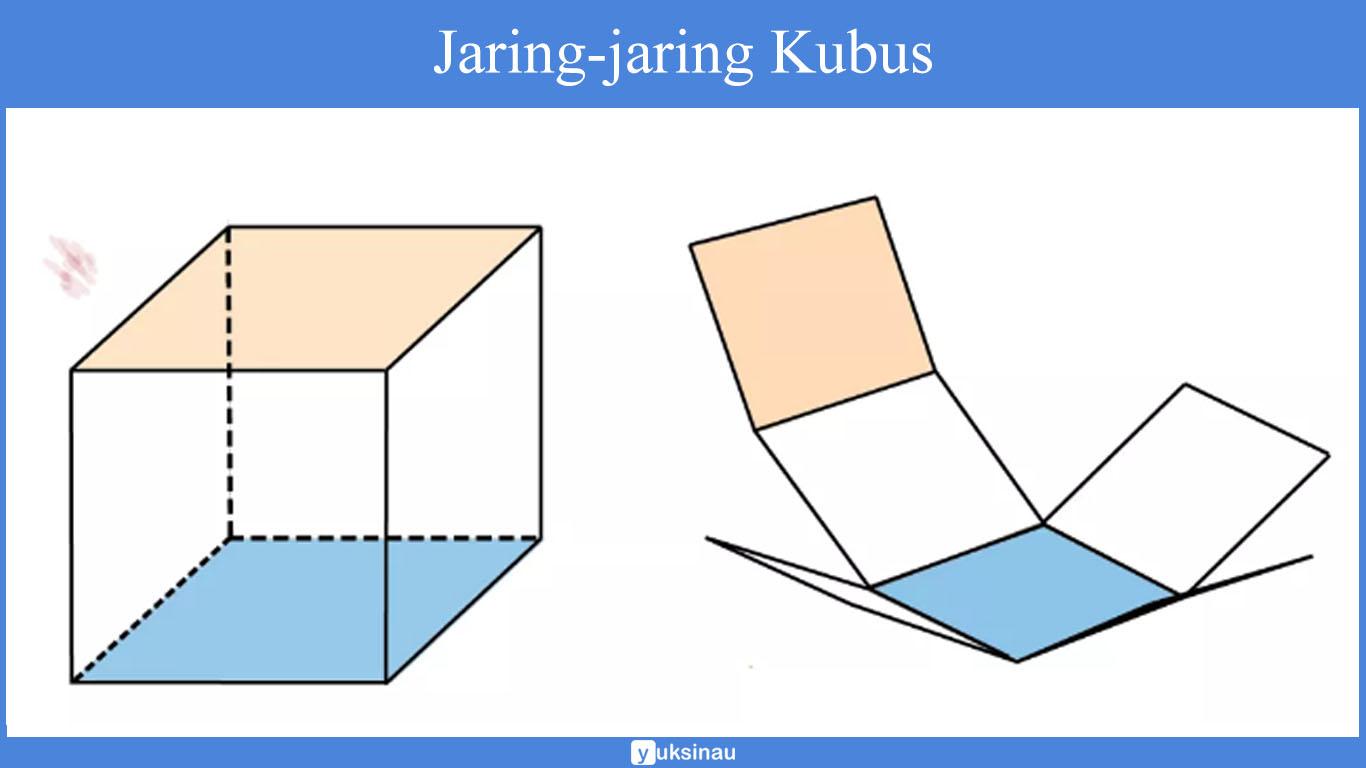
Jika kubus dipotong berdasarkan rusuk-rusuknya, lalu masing-masing sisinya direntangkan maka akan menghasilkan suatu bangun datar yang disebut sebagai jaring-jaring kubus.
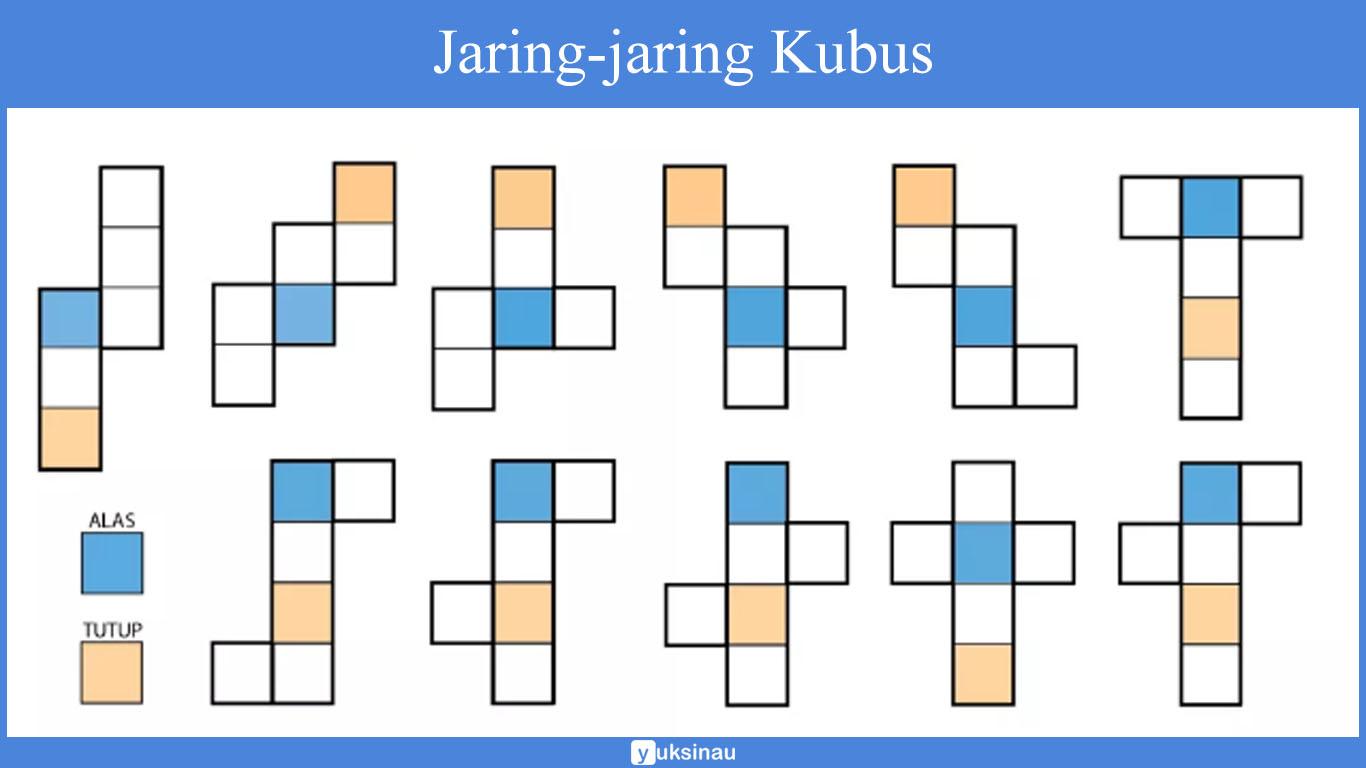
Terdapat sebelas macam jaring-jaring kubus di mana susunannya berbeda satu sama lain. Masing-masing terdiri atas enam buah persegi kongruen yang saling berkaitan.
Simak gambar yang ada di bawah ini:
Rumus Pada Kubus
Volume: s x s x s = s3
Luas permukaan: 6 s x s = 6 s2
Panjang diagonal bidang: s√2
Panjang diagonal ruang: s√3
Luas bidang diagonal: s2√2
Balok
Pengertian Balok
Balok adalah suatu bangun ruang yang mempunyai tiga pasang sisi segi empat. Di mana pada masing-masing sisinya yang berhadapan mempunyai bentuk serta ukuran yang sama.
Berbeda halnya dengan kubus di mana seluruh sisinya kongruen berbentuk persegi, dan pada balok hanya sisi yang berhadapan yang sama besar.
Serta tidak seluruhnya berbentuk persegi, kebanyakan berbentuk persegi panjang.
Bagian Bagian Balok
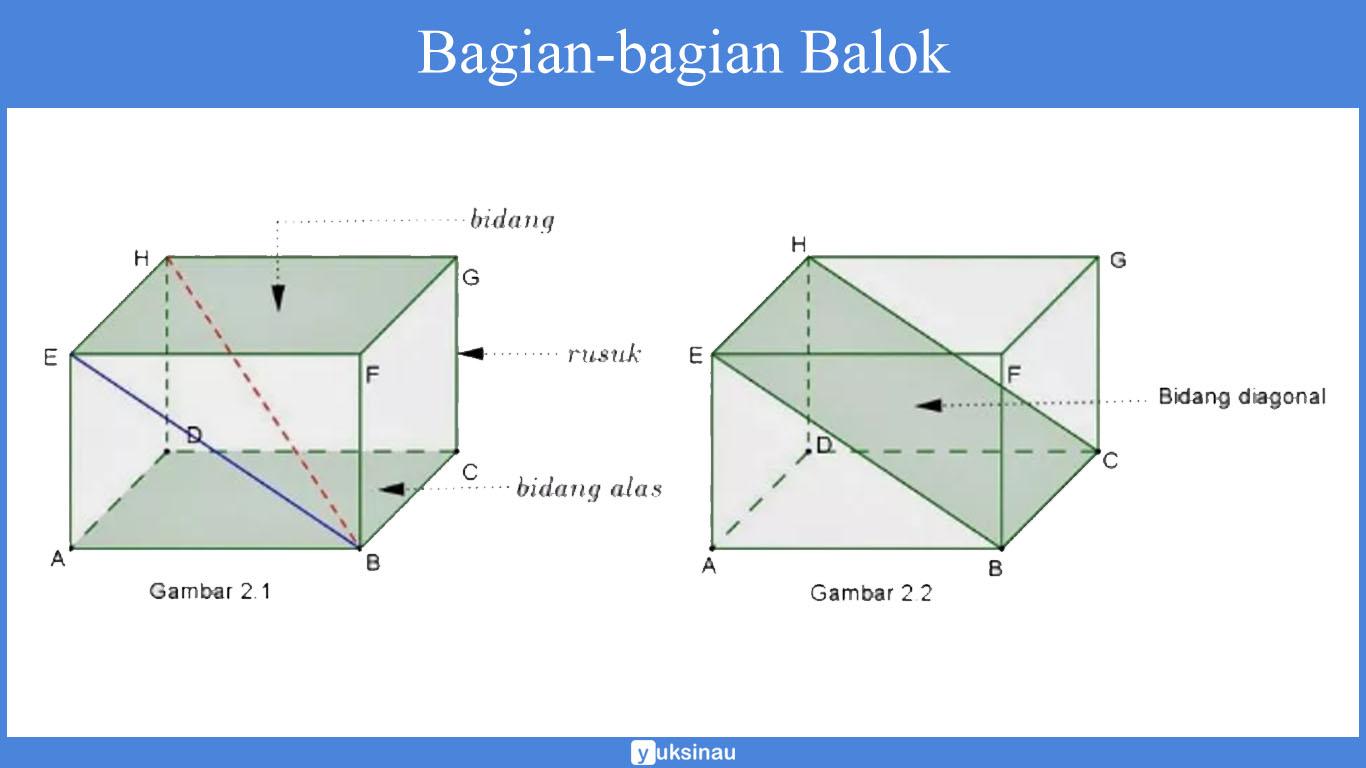
Pada masing-masing dari bangun ruang sisi datar yang satu ini sama seperti yang ada pada kubus.
Suatu balok terdiri tas sisi, sudut, diagonal bidang, diagonal ruang, serta yang terakhir yaitu bidang diagonal.
Berikut akan kami berikan rincian jumlahnya untuk kalian semua:
- Sisi berbentuk persegi dan juga persegi panjang sebanyak 6 buah, antara lain yaitu:
- bidang alas kubus: ABCD
- bidang atas kubus: EFGH
- sisi tegak kubus: ABEF, CDGH, ADEH, dan BCFG.
- Rusuk sebanyak 12 buah yang dapat dibagi menjadi 3 kelompok, antara lain:
- panjang (p) yakni rusuk terpanjang dari alas balok serta rusuk lainnya yang sejajar: AB, DC, EF dan HG
- lebar (l) adalah rusuk terpendek dari alas balok dan juga rusuk lainnya yang sejajar: BC, AD, FG, dan EH
- tinggi (t) adalah rusuk yang tegak lurus terhadap panjang dan lebar balok: AE, BF, CG, dan DH.
- Titik sudut berjumlah 8 titik (A, B, C, D, E, F, G, H).
- Diagonal bidang sebanyak 6 buah (AC, BD, EG, FH, AF, BE, CH, DG, AH, DE, BG, dan CF).
- Diagonal ruang yang berjumlah 4 buah (AG, BH, CE, dan DF).
- Bidang diagonal yang berbentuk persegi panjang dengan jumlah 6 buah, antara lain: ABGH, EFCD, BCHE, FGDA, BFHG, dan AEGC.
Sifat Balok
- Sedikitnya sebuah balok mempunyai dua pasang sisi yang berbentuk persegi panjang.
- Rusuk-rusuk yang sejajar memiliki ukuran yang sama panjang:
AB = CD = EF = GH, dan AE = BF = CG = DH. - Pada masing-masing diagonal bidang pada sisi yang berhadapan berukuran sama panjang, yakni:
ABCD dengan EFGH, ABFE dengan DCGH, dan BCFG dengan ADHE yang mempunyai ukuran sama panjang. - Masing-masing diagonal ruang pada balok mempunyai ukuran sama panjang.
- Masing-masing bidang diagonalnya berbentuk persegi panjang.
Jaring Jaring Balok
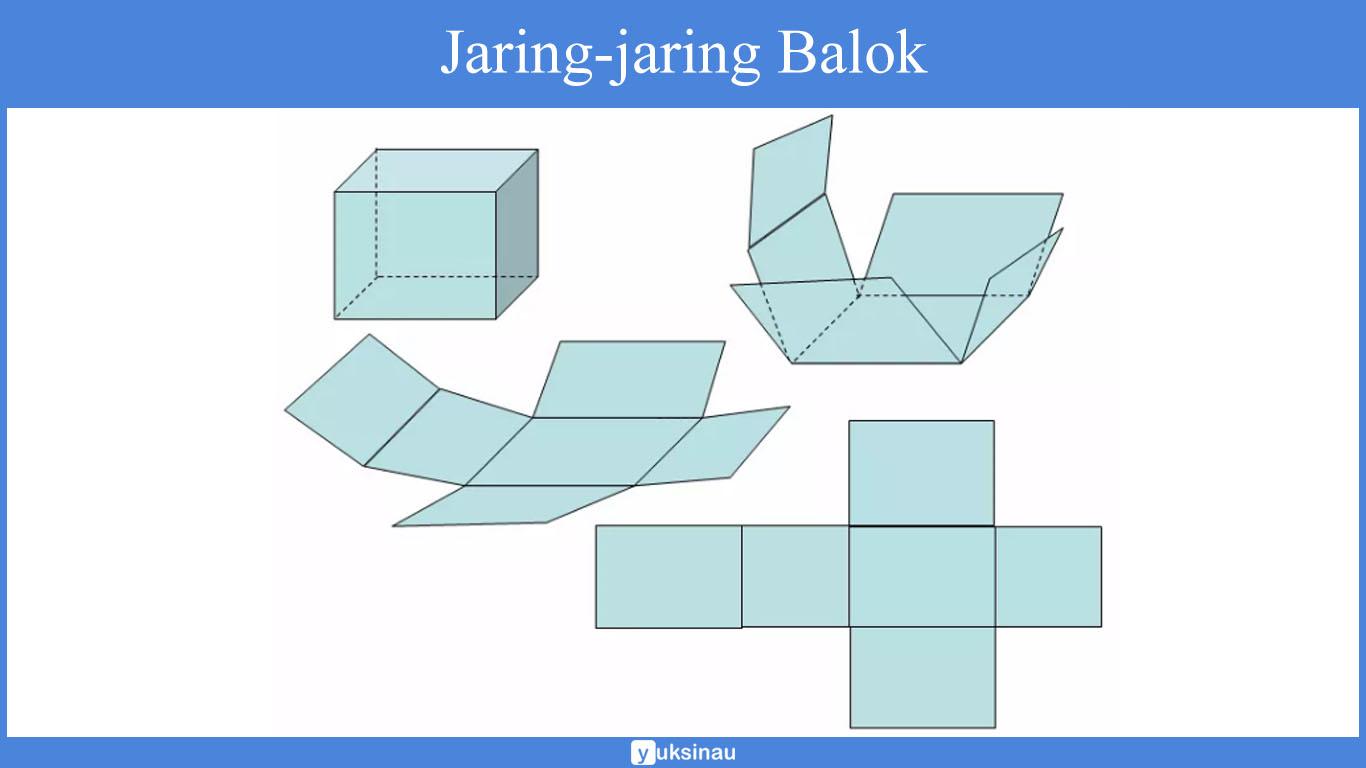
Sama halnya dengan kubus, jaring-jaring pada bangun balok juga didapatkan dengan cara membuka balok tersebut sehingga akan terlihat semua permukaan balok.
Coba kalian perhatikan baik-baik pada jalur pembuatan jaring-jaring balok di atas.
The post Bangun Ruang Sisi Datar appeared first on Tuliskan.
ARTIKEL PILIHAN PEMBACA :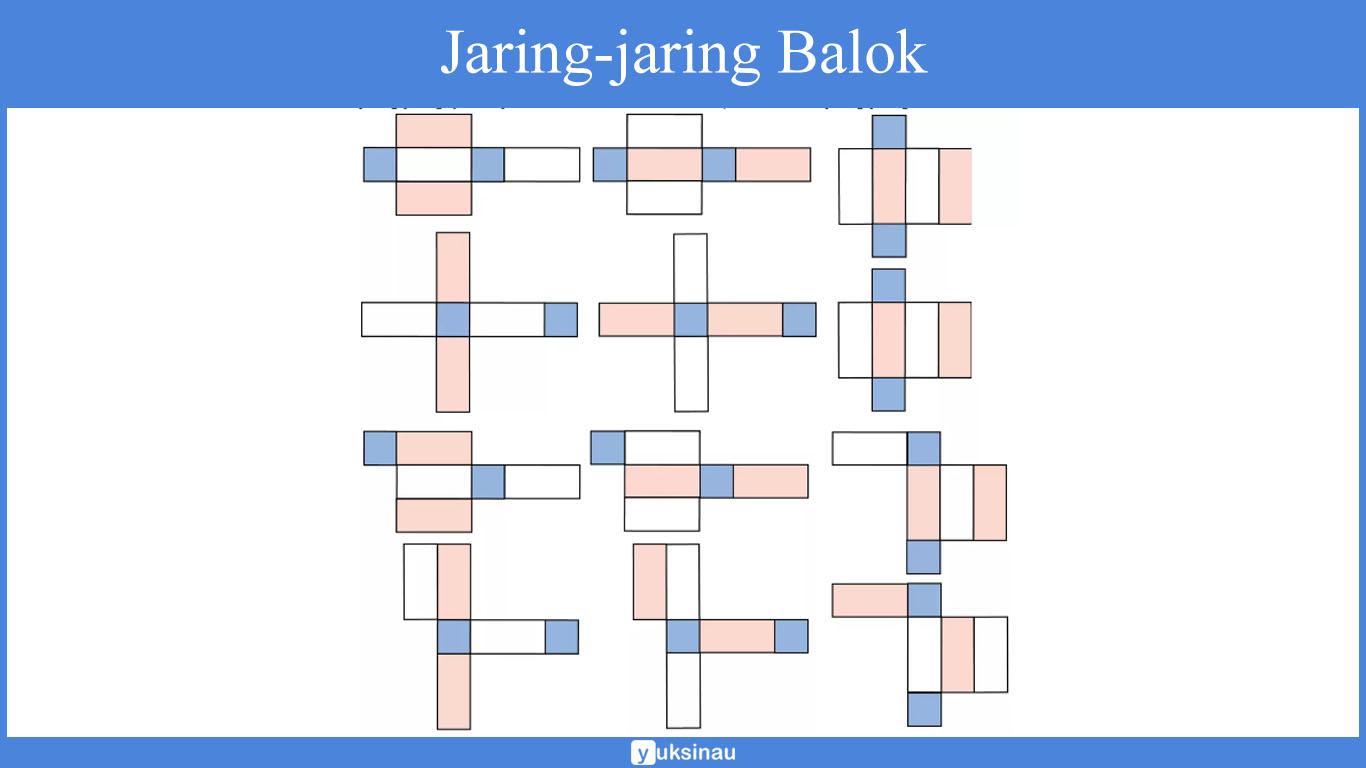

Comments
Post a Comment