Uraian: Rumus Amplitudo (Lengkap)

Rumus Amplitudo - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Rumus Amplitudo?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Rumus Amplitudo ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Rumus Amplitudo

Pada kesempatan kali ini, kita akan membahas secara lebih detail terkait amplitudo, mulai dari pengertian, rumus, hingga contohnya.

Maka dari itu, pastikan kalian simak baik – baik artikel rumus amplitudo ini sampai selesai ya.

Pengertian Amplitudo

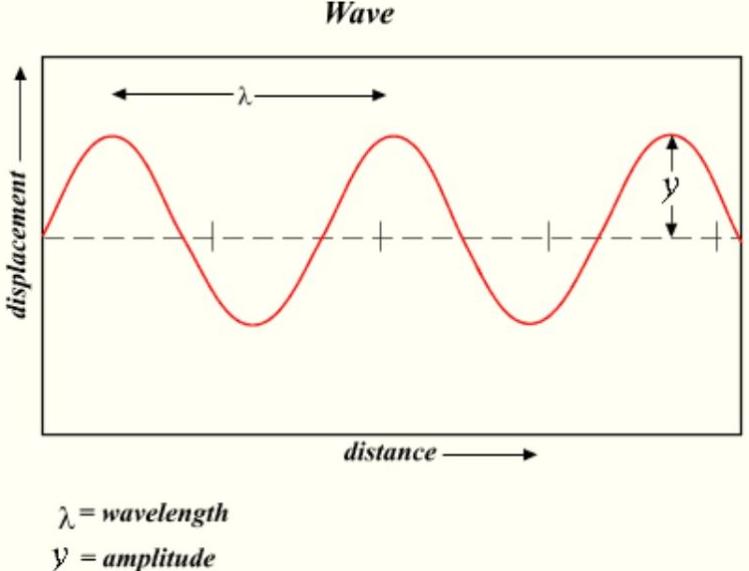
Amplitudo merupakan suatu pengukuran skala yang non-negatif dari besar osilasi sebuah gelombang.

Pada amplitudo ini juga sering kali diartikan sebagai jarak maupun simpangan terjauh dari titik kesetimbangan do di dalam gelombang sinusoide yang akan kalian pelajari dalam mata pelajaran Fisika dan juga Matematika.

Pada umumnya, amplitudo memiliki simbol sistem Internasional berupa (A) dengan satuan meter (m).

Sementara jika amplitudo dalam musik merupakan volume dari suatu sinyal audio.

Suatu gelombang amplitude yang diukur dari jarak garis tengah serta ukuran ini disebut ke dalam satuan Decibel.

Jenis – Jenis Amplitudo

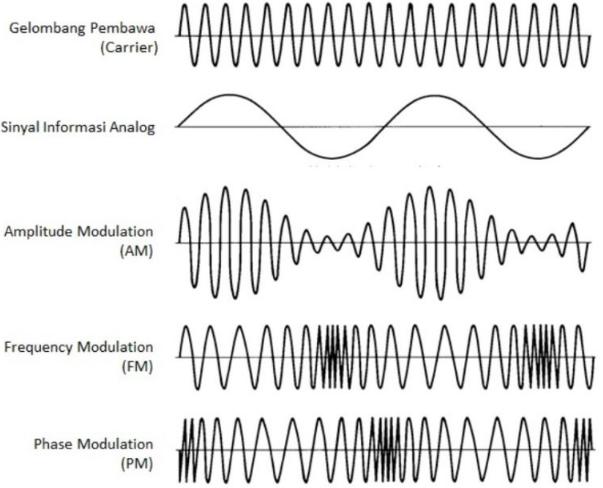
Sebetulnya, jenis amplitudo sendiri ada banyak sekali, namun hanya ada 3 jenis yang utama yang perlu kalian ketahui, antara lain:

• Memiliki jarak terjauh dari titik kesetimbangan ke dalam gelombang sinusoide.
• Memiliki pengukuran skala yang non negatif dari besar osilasi gelombang.
• Memiliki simpangan yang paling besar serta terjauh dari titik kesetimbangan pada gelombang dan juga getaran.

Pola Simpangan

Simpangan atau jarak terjauh mempunyai titik pola yang bermacam – macam, apakah dapat dikatakan sebagai getaran atau gelombang. Berikut penjelasannya:

1. Amplitudo Getaran

Getaran adalah suatu gerak bolak balik yang hanya berlangsung pada sekitar titik kesetimbangan.

Gerak satu ini biasanya hanya akan muncul apabila suatu benda diberikan suatu gaya.

Contoh yang sangat sederhana dari gerak satu ini adalah getaran pada bandul.

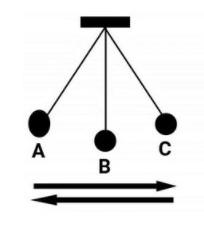
Amplitudo Getaran
A-B = 1/4 Getaran
B-C = 1/4 Getaran
A-B-C = ½ Getaran
A-B-C-B = ¾ Getaran
A-B-C-B-A = 1 Getaran

2. Amplitudo Gelombang

Seperti yang telah disebutkan sebelumnya bahwa gelombang berbeda dengan getaran.

Alasan perbedaan tersebut adalah pola gerak pada gelombang yang bersifat continue serta merambat dari satu titik ke arah titik yang lain.

Pada gelombang sendiri ada dua macam, yakni gelombang transversal dan gelombang longitudinal.

Perbedaan diantara kedua jenis gelombang itu terletak pada arah rambat gelombang nya.

Metode Kuantifikasi Amplitudo Getaran

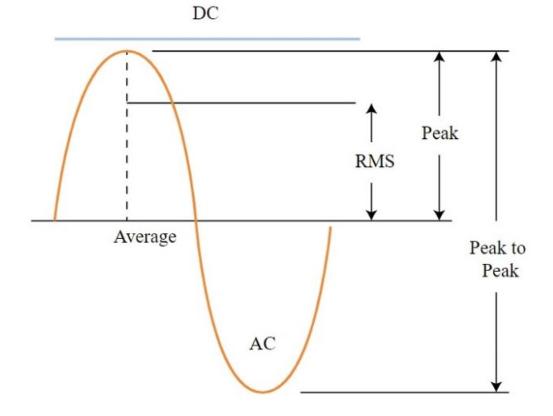
Berikut ini adalah beberapa metode kuantifikasi amplitudo getaran yang perlu kalian ketahui, antara lain:

1. Nilai Puncak (Peak)

Nilai puncak satu ini bermanfaat untuk menunjukkan tingkat guncangan dengan durasi yang pendek.

Namun, untuk nilai puncak hanya akan menunjukkan tingkat maksimum dari getaran yang berlangsung dalam satu titik waktu tertentu.

2. Nilai Puncak ke Puncak (Peak-to-Peak)

Nilai dari amplitudo puncak ke puncak ini memiliki peran yang penting, sebab nantinya akan menunjukkan ekskursi maksimum terhadap gelombang.

Kuantitas satu ini digunakan untuk mengetahui perpindahan bagian mesin akibat dari adanya getaran yang penting untuk menghitung tegangan maksimum di dalam suatu material mesin.

3. Nilai Root Mean Square (RMS)

Nilai Root Mean Square merupakan suatu nilai amplitudo yang sangat relevan, sebab tak hanya digunakan untuk memperhitungkan waktu, namun metode perhitungan RMS yang menguadratkan nilai negatif sinusoidal getaran juga akan memberikan nilai amplitudo yang lebih akurat.

Pada nilai amplitudo Root Mean Square satu ini nantinya akan memberikan informasi nilai kandungan energi terhadap getaran suatu parameter dengan kemampuan destruktif untuk komponen mesin.

4. Nilai Rata – Rata (Average)

Nilai amplitudo rata – rata telah memperhitungkan durasi waktu getaran yang berlangsung.

Namun akan dianggap memiliki fungsi yang terbatas sebab dalam proses perhitungannya nilai negatif terhadap gelombang sinusoidal getaran seakan meniadakan.

Lambang Amplitudo

Gambar Amplitudo

Simbol atau lambang pada amplitudo yang perlu kalian ketahui antara lain ialah sebagai berikut:

Keterangan:

• A = Y/Sin
• Co = Kecepatan
• Y = Simpangan
• A = Amplitudo
• T = Waktu

Gerak osilasi sama seperti bandul atau suatu gerak harmonic yang sederhana.

Rumus Amplitudo

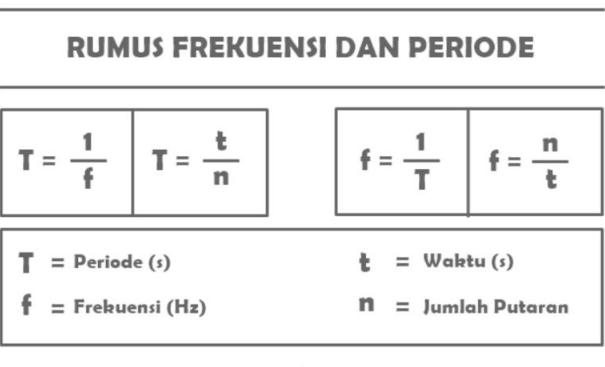
Setelah mengetahui keterangan di atas, di bawah ini adalah beberapa rumus dari Amplitudo yang perlu untuk kalian ketahui, antara lain:

1. Rumus Amplitudo Simpangan Periode Getaran

T = t/n

2. Rumus Frekuensi Getaran Amplitudo

F = n/t

3. Rumus Hubungan antara Frekuensi dan Periode Amplitudo

T = 1/f atau f = 1/T

Pengertian Frekuensi, Getaran & Gelombang

Berikut ini adalah beberapa istilah yang kerap kali disandingkan dengan amplitudo dan perlu untuk kalian ketahui, antara lain:

1. Frekuensi

Frekuensi merupakan suatu jumlah maupun banyaknya getaran yang berlangsung pada waktu kurang lebih dari satu detik.

Satuan untuk frekuensi ialah Hertz (Hz).

Di dalam frekuensi, biasanya dirumuskan dengan (f = N/t) yang mana (N) adalah jumlah terhadap getaran, sementara (t) merupakan simbol waktu.

Sehingga dengan demikian, kalian dapat menyimpulkan bahwa jumlah frekuensi merupakan suatu jumlah getaran yang dibagi dengan jumlah waktu.

2. Getaran

Getaran adalah sebuah gerak bolak – balik yang ada di sekitar kesetimbangan.

Kesetimbangan yang dimaksud ialah di aman kondisi dari sebuah benda dalam posisi diam, jika tidak terdapat gaya yang bekerja di dalam benda tersebut.

Getaran ini memiliki hubungan yang sangat erat dengan frekuensi serta amplitudo.

Satu kali gerak bolak – balik penuh, maka sama halnya dengan satu getaran frekuensi.

3. Gelombang

Gelombang adalah suatu getaran yang merambat. Idealnya, gelombang tersebut akan mengikuti gerak sinusoide.

Pada gelombang dapat berjalan melalui ruang hampa maupun udara serta dapat melalui medium.

Yang mana hal itu dapat bergerak serta dapat memindahkan energi dari suatu tempat menuju tempat yang lainnya.

Tanpa harus melibatkan partikel medium maupun berpindah secara permanen.

Perbedaan Gelombang Berjalan dengan Gelombang Berdiri

Berikut ini adalah perbedaan dari gelombang berjalan dan gelombang berdiri yang perlu kalian ketahui, antara lain:

1. Gelombang Berjalan

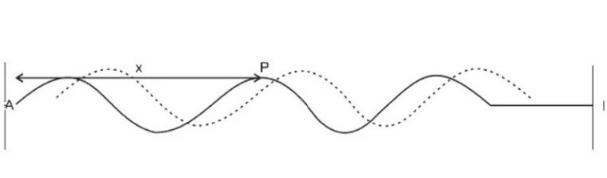
Gelombang berjalan adalah suatu gelombang yang amplitudo serta fasenya tetap pada setiap titik yang dilaluinya.

Simpangan yang ada pada gelombang berjalan memiliki rumus sebagai berikut:

y = A sin ω (t – x/y)
y = A sin 2π/y (t – x/v)
y = A sin 2π (t/T – x/λ)

Yang mana,

k = 2π/λ dan ω = 2πf = 2π/T

Sehingga, persamaan gelombang berjalan tersebut dapat menjadi:

y = ± A sin 2π (t/T +- x/λ)
y = ± A sin (ωt +- kx)

Keterangan:

• Y = Simpangan (m)
• ω = Frekuensi sudut
• A = Amplitudo (m)
• x = Jarak titik ke sumber (m)
• k = Bilangan gelombang
• t = Waktu (s)

Tanda ± memiliki peran sebagai:

• + (Positif) jika gelombang merambat ke arah kanan serta titik asal 0 bergetar ke atas.
• – (Negative) jika gelombang merambat ke arah kiri serta titik asal 0 bergerak ke bawah.

2. Gelombang Berdiri

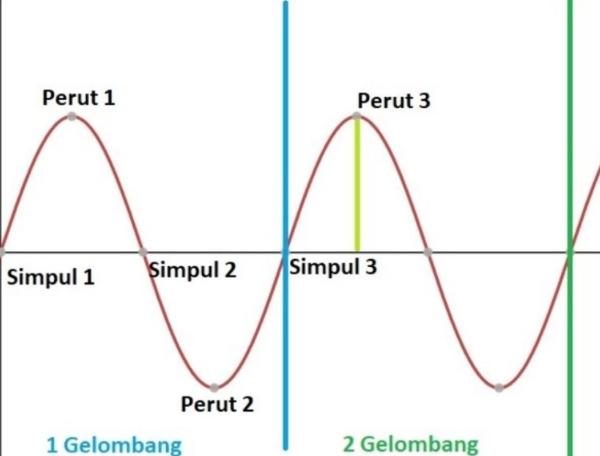
Gelombang berdiri atau juga bisa disebut sebagai gelombang stasioner merupakan suatu gelombang yang amplitudonya berubah – ubah, nilainya mulai dari nol hingga nilai maksimum tertentu.

Sebagai contoh:

Seutas tali yang salah satu ujungnya diikatkan pada sebuah tiang serta ujung lainnya digerakkan ke atas dan juga ke arah bawah.

Gelombang tali tersebut nantinya akan merambat dari ujung tali yang digetarkan menuju ujung tali yang terikat serta akan dipantulkan kembali menuju arah semula.

Pada gelombang datang serta gelombang pantul saling berinterferensi sejingga disebut sebagai gelombang berdiri.

Gelombang berdiri terdiri atas simpul dan perut, yaitu:

• Simpul merupakan tempat kedudukan titik yang amplitudonya minimum.
• Perut merupakan tempat kedudukan titik yang amplitudonya maksimum dalam sebuah gelombang.

Di dalam gelombang berdiri ini juga dibagi lagi menjadi dua bagian berbeda, yakni:

a. Ujung bebas

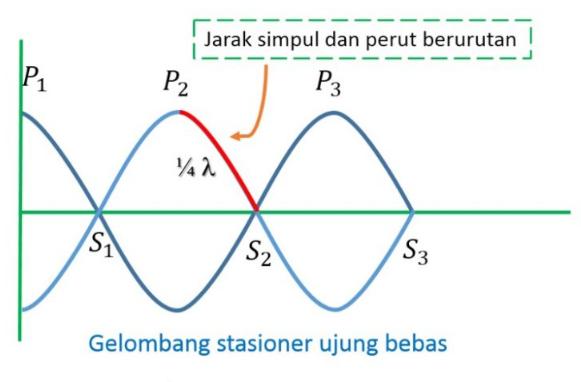
Gelombang berdiri dalam ujung bebas ini memiliki fase gelombang datang sama dengan gelombang pantul.

Ujung pemantul dapat bergerak secara bebas naik maupun turun dengan mengikuti arah getar gelombang yang datang.

Untuk besar simpangannya sendiri ialah sebagai berikut:

y = 2 A cos kx sin ωt

Simpul → x = (2n + 1) λ/4 dengan n = 0,1,2,3,…

Perut → x = 1/2nλ dengan n = 0,1,2,3,…

b. Ujung Terikat

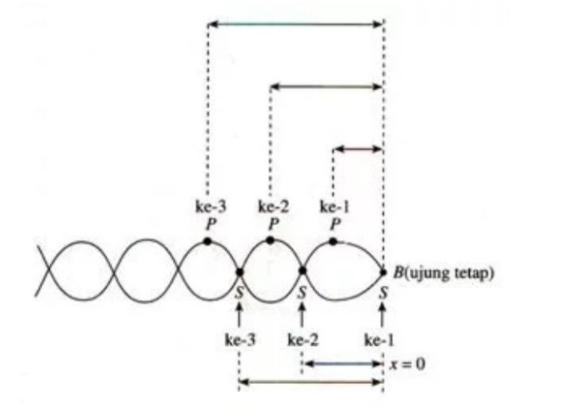
Gelombang berdiri bersama ujung terikat memiliki sudut fase gelombang datang serta gelombang pantul yang berbeda besar dari radian nya.

Ujung pemantul tidak dapat bergerak bebas dengan mengikuti arah getar gelombang datang.

Besar simpangan terhadap gelombang berdiri ujung terikat ialah sebagai berikut:

y = 2 A sin kx cos ωt

Simpul → x = 1/2n λ dengan n = 0,1,2,3,…

Perut → xn+1 = (2n + 1) λ/4 dengan n = 0,1,2,3,…

Contoh Soal

Untuk mempermudah kalian dalam memahami uraian yang ada di atas, berikut ini kami berikan beberapa contoh soal beserta penjelasannya yang dapat kalian pelajari, antara lain:

1. Contoh Pertama

Sebuah gelombang mempunyai persamaan y = 2 sin 1/12 π yang mana y dalam meter serta t dalam detik.

Hitunglah besar amplitudo, periode, serta simpangan pada waktu t 2 detik.

Jawab:

y = 2sin1/12 πt
y = Asin2πft
Amplitudo = 2 m

1/12 π = 2πf
f = (1/12)(π)/(2π)
f = 1/24 Hz

T = 1/f
T = 1/(1/24)
T = 24 s

y = 2sin((1/12) (πt))
y = 2sin((1/12) (2π))
y = 2sin(π/6)
y = 2sin30°
y = (2)(1/2) y = 1 m.

2. Contoh Kedua

Terdapat suatu tali yang bergetar sebanyak = 60 kali dengan durasi selama 0,5 menit.

Cari dan juga hitunglah periode getar pada seutas tali tersebut!

Jawab:

Diketahui:

n = 60
t = 0,5 menit = 0,5 x 60 = 30 sekon

Ditanya:

Cari periode getar (T).

Penjelasan:

T = t/n
T = 30/60
T = 1/2 = 0,5 sekon

Sehingga, periode getar pada seutas tali yang dihasilkan ialah 0,5 sekon.

3. Contoh Ketiga

Seutas tali memiliki panjang 3 m dengan ujung ikatannya bisa bergerak serta ujung lainnya digetarkan dengan besar frekuensi 8 Hz sehingga gelombang dapat merambat dengan kelajuan 3 m/s.

Jika diketahui amplitudo gelombang sebesar 20 cm, berapa persamaan simpangan super posisi gelombang pada titik P dengan jarak 1 meter dari ujung pemantulan?

Jawab:

Diketahui:

• l = 3 m
• f = 8 Hz
• v = 3 m/s
• A = 20 cm = 0,2 m
• x = 1 m

Ditanya:

Persamaan persimpangan (y).

Penjelasan:

ω = 2π f = 2π8 = 16π rad/s
y = 2 A cos (kx) sin (ωt – 2πl/λ)
y = 2 (0,2) cos (16π/3(1)) sin (16πt – 2π(3)/3/8)
y = 0,4 cos (16π/3) sin (16πt – 40π/3)
y = 0,4 cos 2π (8/3) sin 2π (8t – 20/3)

4. Contoh Keempat

Terdapat seutas tali yang bergetar sebanyak = 90 kali dengan durasi selama 0,5 menit.

Cari dan juga hitung frekuensi getar seutas tali tersebut!

Jawab:

Diketahui:

n = 90
t = 0,5 menit (diubah menjadi sekon) = 0,5 x 60 = 30 sekon

Ditanya:

f =…?

Penjelasan:

f = n/t
f = 90/30 = 3 hz

Sehingga dapat diketahui bahwa frekuensi getar seutas tali tersebut ialah = 3 hz.

5. Contoh Kelima

Terdapat seutas tali yang bergetar sebanyak = 90 kali dengan durasi selama = 0,5 menit.

Cari dan juga hitunglah periode getar pada seutas tali tersebut!

Jawab:

Diketahui:

n = 90
t = 0,8 menit (diubah menjadi sekon) = 0,5 x 60 = 30 sekon

Ditanya:

T =…?

Penjelasan:

T = t/n
T = 30/90
T = 1/3 = 0,33 sekon

Sehingga dapat diketahui bahwa periode getar seutas tali tersebut ialah = 0,33 sekon.

The post Rumus Amplitudo appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Rumus Amplitudo (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.