Uraian: Lingkaran (Lengkap)

Lingkaran - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Lingkaran?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Lingkaran ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Lingkaran

Sering sekali kita mendangar isitlah lingkaran? Lantas apa yang dimaksud dengan lingkaran? Lingkaran dalam matematika merupakan sebuah bangun datar dua dimensi.

Lingkaran juga merupakan sekumpulan dari titik – titik yang membentuk suatu lengkungan yang memiliki panjang yang sama pada titik pusat lingkaran.

Lengkungan – lengkungan yang terdapat dalam lingkaran saling berkaitan serta mengelilingan titik pusat dan juga membentuk daerah di dalamnya.

Suatu bentuk lingkaran pasti memiliki luas dan juga keliling.

Adapun rumus untuk  luas lingkaran yaitu π × r² . Sementara untuk rumus pada keliling lingkaran bis kita cari dengan memakai rumus  2 × π × r.

Namun, khusus untuk pembhasan rumus akan kita ulas selengkapnya pada sub berikutnya.

Pada setiap rumus lingkaran tak lepas pasti memakai lambang π atau apabila kita baca akan berbunyi “phi” yang mana nilai dari phi tersebut yaitu 22/7 atau 3,14.

Hal tersebut tergantung pada koefisien jari-jari. Dan juga nilai tersebut sudah merupakan nilai ketetapan yang tidak dapat diotak-atik dengan sendiri.

Unsur Unsur Lingkaran Matematika

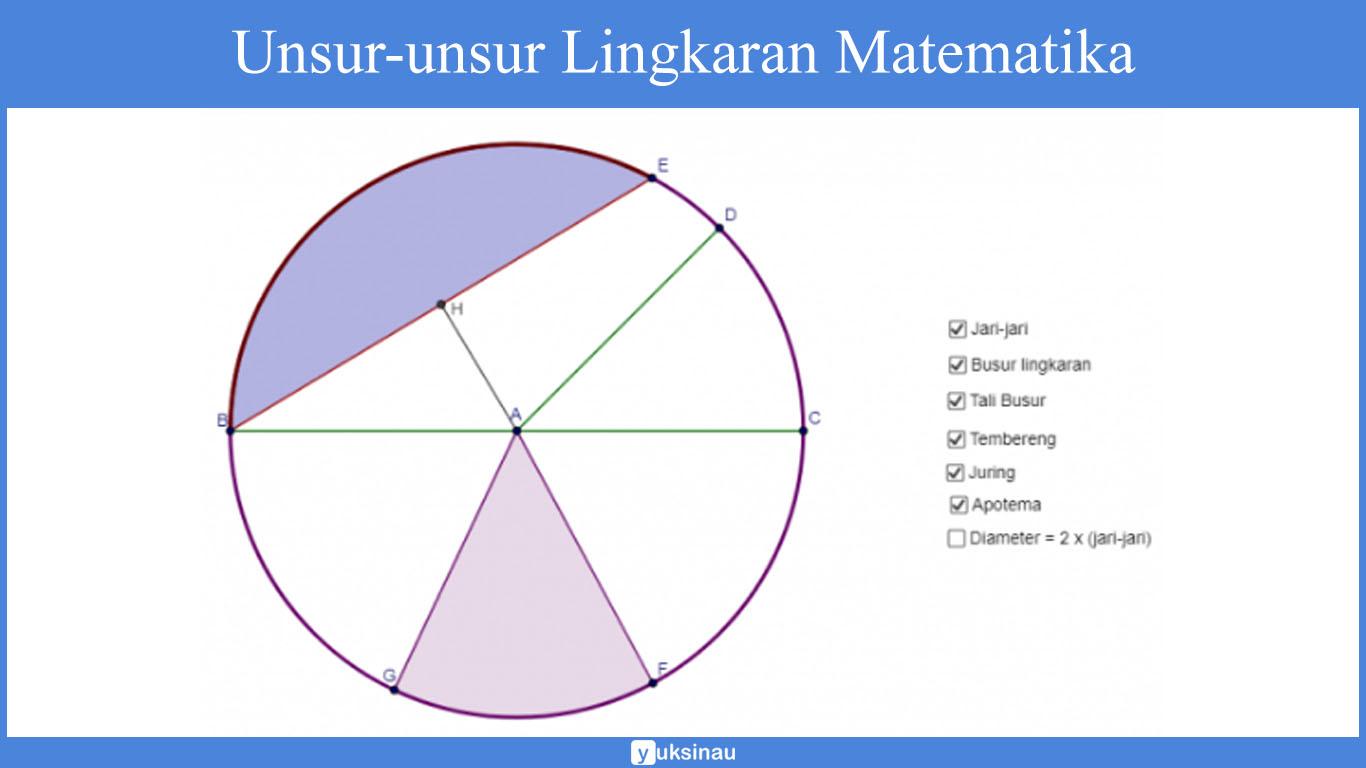
Sebuah lingkaran pastilah mempunyai beberapa bagian – bagian di dalamnya. Bagian tersebut meliputi: diameter, jari – jari, tembereng, juring, dan yang lainnya.

Di dalam sebuah lingkaran terdapat 10 unsur. Untuk lebih memahami dengan lebih jelas lagi tetang unsur – unsur yang terkandung di dalam lingkaran. Berikut akan kami berikan penjelasan pada masing-masing unsur – unsur yang ada di dalam lingkaran, antara lain:

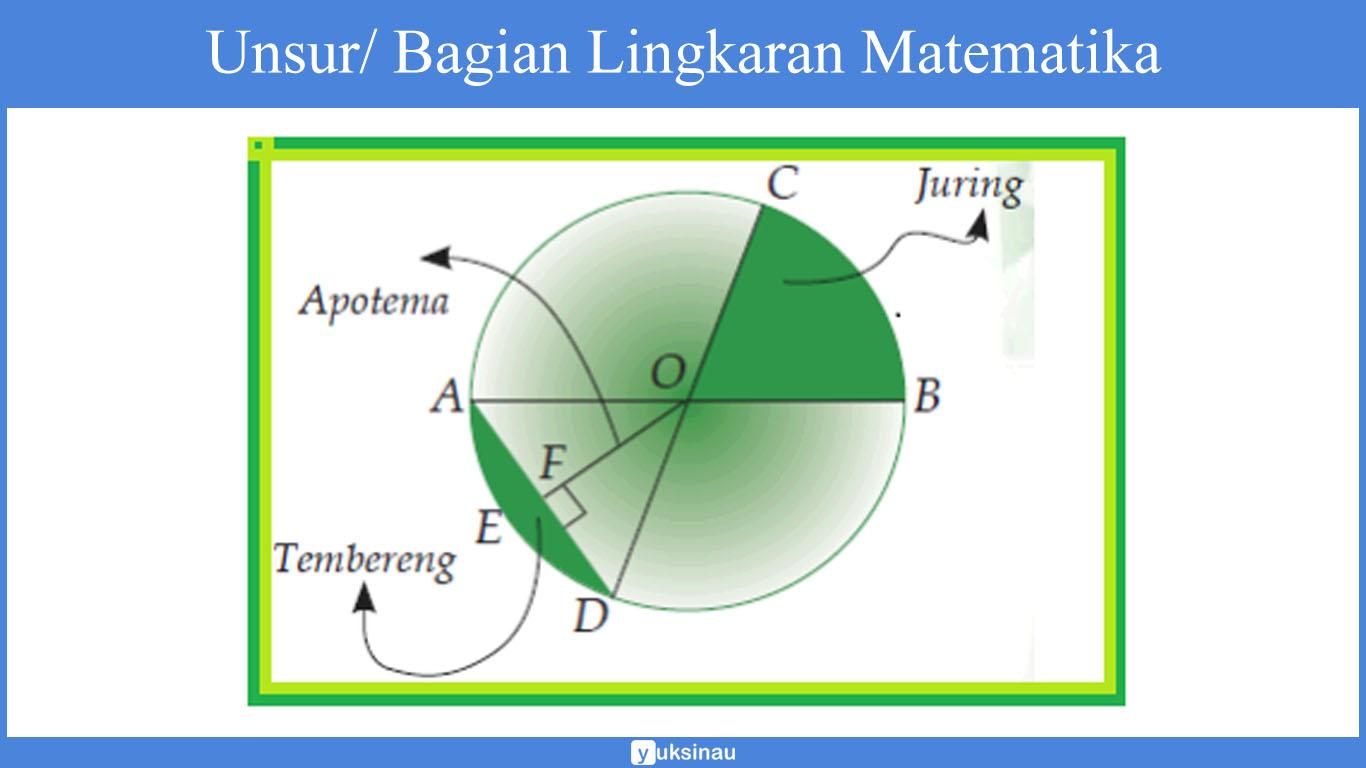
1. Jari-jari Lingkaran

Jari – jari dalam lingkaran merupakan suatu garis yang menghubungkan antara titik pusat dengan titik pada keliling lingkaran.

Pada gambar di atas, jari – jari lingkaran berada pada garis OC, OD, OB dan juga OA.

2. Titik Pusat Lingkaran

Titik pusat yang terdapat dalam lingkaran merupakan suatu titik yang berada tepat ditengah – tengah lingkaran.

Pada gambar lingkaran di atas, titik pusat lingkaran terletak di huruf O.

3. Busur Lingkaran

Yang dimaksud dari busur pada lingkaran yaitu suatu garis lengkung yang di mana adalah bagian dari keliling lingkaran.

Busur pada lingkarang terbagi menjadi dua macam, antara lain: busur besar dan busur kecil.

Disebut sebagai busur besar apabila panjangnya lebih dari setengah lingkaran.

Sementara disebut sebagai busur kecil apabila panjangnya kurang dari setengah lingkaran. Pada gambar di atas, busur lingkarang berada di garis lengkung AC, CB, BD, dan juga AD.

4. Diameter Lingkaran

Yang disebut sebagai diameter pada lingkaran yaitu suatu panjang garis lurus yang mengaitkan antara dua titik pada keliling lingkaran yang melewati titik pusat lingkaran.

Dari definisi tersebut, maka dapat kita ambil kesimpulannya jika jari – jari lingkaran mempunyai nilai setengah dari diameter atau diameter mempunyai nilai dua kali dari jari – jari.

Sehingga rumus yang ditulis yaitu d = 2r.

Pada gambar di atas, diameter lingkaran atau garis tengah lingkaran berada tepat di garis AB dan CD.

5. Tembereng Lingkaran

Pengertian dari tembereng pada lingkaran yaitu daerah yang terletak di dalam lingkaran yang telah dibatasi oleh busur lingkaran serta tali busur lingkaran.

Pada gambar di atas, tembereng lingkarang telah dibatasi oleh busur AD dan juga tali busur AD.

6. Tali Busur Lingkaran

Yang dimaksud dari tali busur pada lingkaran yaitu garis lurus yang mengaitkan dua titik pada keliling lingkaran serta tidak melewati titik pusat lingkaran.

Apabila kita ibaratkan, tali busur lingkaran seperti halnya tali yang terdapa pada busur panah.

Pada gambar di atas, tali busur lingkaran berada pada garis AD.

7. Apotema Lingkaran

Unsur selenjutnya ialah Apotema Lingkaran.

Apotema lingkaran merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran.

Garis apotema pada umumnya terletak tegak lurus dengan tali busur.

Pada gambar di atas, garis apotema berada di garis OF.

8. Juring Lingkaran

Yang dimaksud dengan juring pada lingkaran yaitu suatu daerah yang dibatasi oleh dua garis jari – jari serta telah dibatasi oleh sebuah busur lingkarang yang posisinya diapit oleh dua buah jari – jari tersebut.

Juring lingkarang juga terbagai menjadi dua macam. Antara lain: juring kecil dan juring besar.

Pada gambar di atas, daerah juring lingkaran berada di daerah yang diberi warna hijau yakni juring BOC.

9. Sudut Keliling Lingkaran

Unsur lingkaran selanjutnya yaitu sudut keliling.

Pengertian dari sudut keliling pada lingkaran yakni sudut yang terbentuk sebab adanya pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran.

Apabila kita perhatikan pada gambar di atas, tali busur AC serta tali busur BC yang bertemu di titik C serta membentuk sudut keliling ACB.

10. Sudut Pusat Lingkaran

Unsur yang terakhir yaitu sudut pusat.

Sudut pusat adalah sudut yang terbentuk dari perpotongan antara dua buah jari – jari (OA dan OB) pada titik pusat lingkaran.

Pada gambar di atas, sudut pusat yang terbentuk antara titik A, O, serta B yakni <AOB.

Baca juga: Bangun Ruang Sisi Lengkung

Rumus Lingkaran Matematika

Rumus lingkaran sebetulnya telah kita pelajari saat kita duduk di bangku sekolah dasar.

Tetapi, rumus lingkaran sering kali mengecoh sebab rumus luas dan juga rumus keliling lingkaran yang sekilas terlihat hampir sama.

Oleh sebab itu kita butuh adanya pemahaman yang teliti sehingga tidak akan mudah terkecoh oleh dua rumus tersebut yang hampir sama.

Maka dari itu, mari kita pelajari rumus-rumus lingkaran bersama agar pemahaman tentang lingkaran akan lebih mendalam.

Beberapa rumus yang akan kita pelajari diantaranya yaitu:

1. Rumus luas lingkaran.
2. Rumus keliling lingkaran dengan jari-jari.
3. Rumus lingkaran dengan diameter.
4. Rumus diameter lingkaran.

Yuk langsung saja simak baik-baik ulasan di bawah ini.

Rumus Luas Lingkaran

Luas lingkaran dapat kita hitung dengan menggunakan rumus di bawah ini:

Luas lingkaran: π × r²

Keterangan:

• π = phi = 3,14 atau 22/7
• r = jari-jari, (satuan yang dipakai di mana tergantung dari soal yang dibrikan, bisa cm, dm maupun m. Serta satuan luas yaitu kuadrat atau persegi, contohnya: cm² atau m²)

Contoh Soal dan Pembahasan Luas Lingkaran

Soal 1.

Apabila diketahui sebuah lingkaran memiliki diameter 28 cm. Berapakah luas lingkaran tersebut?

Jawab:

Diketahui:

• d = 28 cm
• d = 2 x r
• r = d/2
• r = 28/2
• r = 14 cm

Ditanyakan:

• Luas lingkaran?

Penyelesaian:

Luas = π × r²

Luas = 22/7 × 14²

= 22/7 x 196

= 22 x 28 = 616 cm²

Sehingga, luas lingkaran tersebut yaitu 616 cm².

Soal 2.

Sebuah lingkaran mempunyai jari-jari sebesar 20 cm. Hitunglah luas lingkaran tersebut?

Jawab:

Diketahui:

• r = 20 cm

Ditanyakan:

• Luas lingkaran?

Penyelesaian:

Luas = π × r²

= 3,14 × 200

= 628 cm²

Sehingga, luas lingkaran tersebut yaitu 628 cm².

Baca juga: Garis dan Sudut

Rumus Keliling Lingkaran dengan Jari-Jari

Pada waktu kita mencari keliling lingkaran, maka terdapat dua rumus yang dapat kita pakai.

Diantaranya:

Rumus pertama yang kita pakai apabila lingkaran tersebut telah diketahui diameternya.

Serta rumus kedua kita pakai dalam menghitung keliling lingkaran yang belum diketahui diameternya.

Berikut adalah pembahasan sekaligus contohnya.

Apabila diameternya tidak diketahui maka kita dapat memakai jari-jari untuk menghitung keliling lingkaran. Rumus yang digunakan ialah sebagai berikut:

Keliling ligkaran: 2 × π × r

Keterangan:

k = Keliling lingkaran

π = phi; nilainya 22/7 atau 3,14

r = jari-jari lingkaran

Contoh Soal dan Pembahasan Keliling Lingkaran dengan Jari-jari

Agar lebih memahami cara untuk menghitung keliling lingkaran maka berikut akan kami berikan contoh soal sekaligus pembahasannya:

Soal 1.

Terdapat suatu lingkaran dengan jari-jari 50 cm, hitunglah keliling lingkaran tersebut!

Jawab:

Diketahui:

• r = 50 cm
• π = 22/7 atau 3,14

Sehingga,

k = 2 x π x r

= 2 x 3,14 x 50

= 314 cm

Maka dari itu, keliling dari lingkaran tersebut yaitu 314 cm.

Soal 2.

Terdapat sebuah lingkaran dengan jari-jari 49 cm, hitunglah keliling lingkaran tersebut!

Jawab:

Diketahui:

• r = 49 cm
• π = 22/7 atau 3,14

Sehingga,

k = 2 x π x r

= 2 x 22/7 x 49

= 2 x 22 x 7 = 308 cm

Maka dari itu, keliling lingkaran tersebut yaitu 308 cm.

Rumus Keliling Lingkaran Dengan Diameter

Rumus ini berlaku apabila yang diketahui merupakan diameter lingkarannya. Untuk menghitung keliling dari sebuah lingkaran dengan memakai diameter, maka kita gunakan rumus sebagai berikut:

Keliling Lingkaran: k = π × d

Keterangan:

k = keliling lingkaran

π = phi =22/7 atau 3,14

d = diameter

Contoh Soal dan Pembahasan Keliling Lingkaran dengan Diamater

Soal 1. 

Berapa keliling lingkaran apabila telah diketahui diameternya 30 cm?

Jawab:

Keliling = π x d

= 3,14 x 30

= 94,2 cm

Sehingga, keliling lingkaran tersebut yaitu 94,2 cm

Soal 2.

Berapa keliling lingkaran apabila diameternya 105 cm?

Jawab:

Keliling = π x d

= 22/7 x 105

= 330 cm

Sehingga, keliling lingkaran tersebut yakni 330 cm.

Rumus Diameter Lingkaran

Jika yang diketahui yaitu keliling dari lingkarannya maka rumus yang kita pakai yaitu rumus diameter lingkaran seperti yang tertera di bawah ini:

d = keliling/ π

Keterangan:

d = diameter

π = phi, nilainya 22/7 atau 3,14

Keliling = keliling lingkaran yang sudah ada

Contoh Soal dan Pembahasan Diameter Lingkaran Matematika

Berikut merupakan contoh soal dan pembahasan dalam mencari diameter lingkaran, antara lain:

Soal 1.

Terdapat suatu papan berbentuk lingkaran dengan keliling 95 cm. Hitunglah diameternya!

Jawab:

Diketahui:

• Keliling = 95 cm
• Diameter?
• Rumus keliling = π x d

Apabila yang diketahui merupakan kelilingnya, maka akan kita pakai rumus seperti berikut ini:

d = keliling / π

Sehingga,

d = 95/3,14 = 30, 25 cm

Maka dari itu, diameter lingkaran tersebut yaitu 24,5 cm.

Soal 2.

Diketahui suatu lingkaran mempunyai keliling sebesar 66 cm. Berapakah diameter lingkaran tersebut?

Jawab:

Diketahui:

• Keliling = 66 cm

Ditanyakan:

• Diameter lingkaran?

Penyelesaian:

Keliling = π × d

Sehingga,

d = keliling / π

= 66 / (22/7)

= (66 × 7) / 22 = 21 cm

Maka dari itu, diameter lingkaran tersebut yakni 21 cm.

Soal lainnya.

Sebuah lingkaran mempunyai diameter 14 cm. Hitunglah Luas dan juga Keliling lingkaran tersebut!

Jawab:

L = π × r² (Ingat bahwa panjang diameter adalah 2x jari-jari lingkaran)

= 22/7 x 72 x 1 cm2

= 154 cm2

Sehingga, luas daerah lingkaran tersebut yaitu 154 cm2.

K = 2 × π × r

= 2 x 22/7 x 7 cm

= 44 cm

Sehingga, panjang keliling lingkaran tersebut yaitu 44 cm.

Baca juga: Teorema Phytagoras

Demikianlah ulasan singkat kali ini mengenai Lingkaran Matematika yang dapat kami sampaikan. Semoga ulasan di atas mengenai mengenai Lingkaran Matematika dapat kalian jadikan sebagai bahan belajar kalian.

The post Lingkaran appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Lingkaran (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.