Uraian: Pengenalan Variabel (Lengkap)

Pengenalan Variabel - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Pengenalan Variabel?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Pengenalan Variabel ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Pengenalan Variabel

Di bangku kelas tujuh (7) dalam mata pelajaran matematika kita akan mempelajari mengenai pengenalan variabel.

Pengenalan variabel ini meliputi variabel, koefisien, konstanta, serta suku. Informasi selengkapnya, simak ulasan selengkapnya mengenai Pengenalan Variabel berikut ini.

Aljabar

Secara bahasa, aljabar berarti mempersatukan berbagai bagian yang terpisah. Dalam hal ini, bagian yang dimaksud meliputi unsur-unsur penyusun suatu bilangan aljabar. Seperti: variabel, koefisien, konstanta, suku, faktor, suku sejenis, suku tidak sejenis.

Untuk lebih memahami mengenai aljabar berikut adalah penjelasannya untuk masing-masinng unsur penyusun dari aljabar.

1.   Variabel

Variabel merupakan suatu lambang pengganti pada suatu bilangan yang belum diketahui nilainya dengan jelas.

Variabel disebut juga seabgai peubah, pada umumnya variable ini dilambangkan dengan huruf kecil seperti  a, b, c, … z.

2.  Koefisien

Koefisien merupaan bilangan yang memuat variabel dari sebuah suku pada bentuk aljabar.

3.  Konstanta

Suku dari suatu bentuk aljabar yang berwujud bilangan serta tidak memuat variabel disebut sebagai konstanta.

4.  Suku

Suku merupakan variabel sekaligus koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.

Pada ulasan sebelumnya, kita telah mempelajari perkalian suatu bilangan bulat, yakni penjumlahan berulang dari bilangan bulat tersebut.

Sebagai contoh:

3 x 4 = 4 + 4 + 4
4 x 5 = 5 + 5 + 5
6₃ = 6 x 6 x 6

Jika bentuk perkalian di atas kita uraikan dalam dalam bentuk aljabar maka akan kita dapatkan berbagai bentuk seperti di bawah ini:

3 x a = a + a + a = 3a
4 x x = x + x + x + x = 4x
4 x p = p + p + p + p = 4p
y3 = y x y x y

Bentuk dari 3a, 4x, y3, 5×2 + 4, dan yang lainnya tersebut disebut sebagai bentuk aljabar. Suatu bentuk aljabar yang memuat huruf dan bilangan. Huruf tersebut disebut sebagai variabel. Bilangan pada bentuk aljabar yang mengandung variabel, disebut sebagai koefisien, sementara bilangan yang tidak mengandung variabel disebut sebagai konstanta.

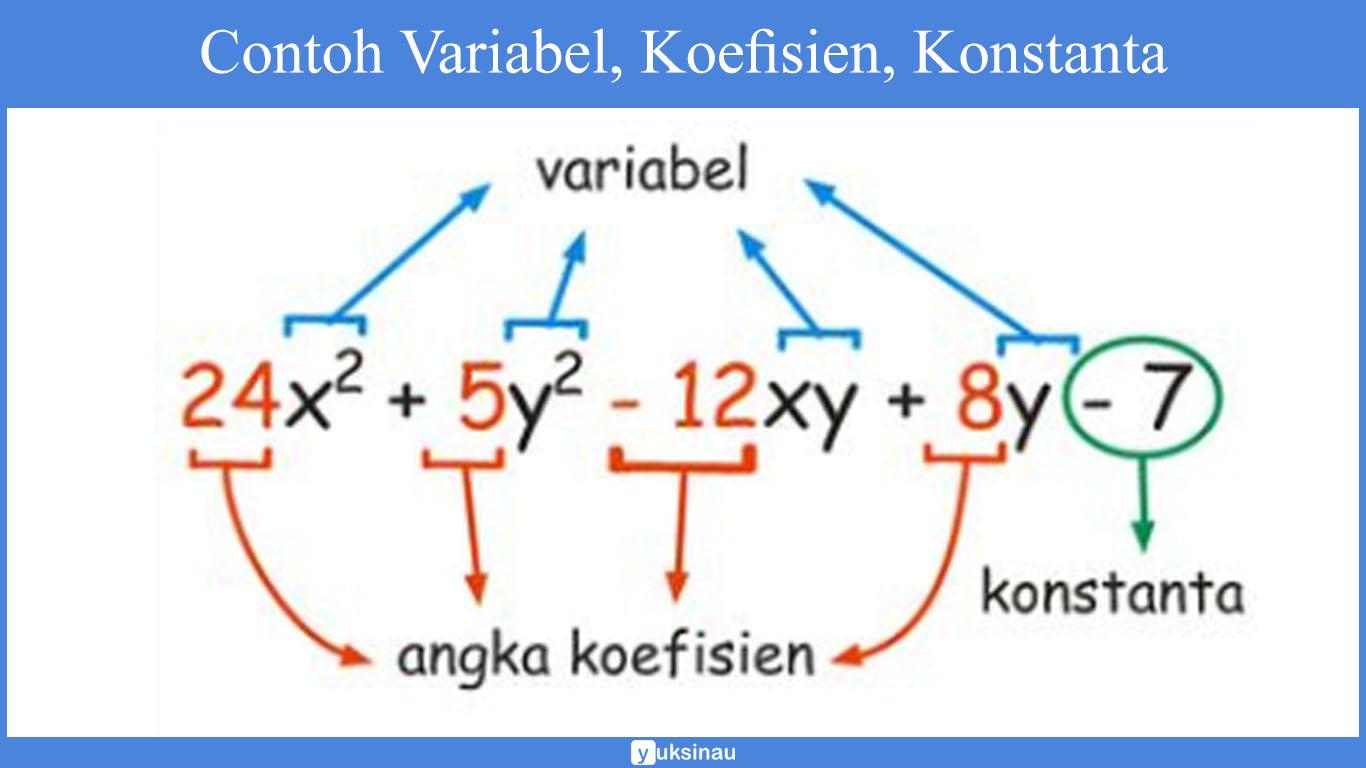
Contohnya:

1. Pada bentuk aljabar 3a, 3 disebut seabgai koefisien a dan a disebut seabgai variabel.
2. Pada bentuk aljabar 2n + 5, 2 disebut sebagai koefisien n, n disebut variabel, dan 5 disebut sebagai konstanta.

Pada bilangan bulat, jika kita tuliskan a = b x c, maka b dan c disebut sebagai faktor-faktor dari a. Sementara dalam bentuk aljabar, jika kita tuliskan 3 (x + 2), maka 3 dan (x + 2) disebut sebagai faktor-faktor perkalian.

Contoh Suku

Perhatikan bentuk aljabar berikut.

5x² + 2x + 7y – 3y + 10

Bentuk aljabar di atas terdiri atas 5 suku, antara lain: 5x², 2x, 7y, –3y, dan 10. Bentuk ini mempunai satu suku sejenis, yakni 7y serta –3y.

Pada bentuk aljabar, suku-suku yang sejenis hanya berbeda pada koefisiennya saja.

Ingin mempelajari rumus pelajaran seperti matematika, fisika, kimia? Pelajari di rumuspintar.com

Contoh Soal Bentuk Aljabar

Soal 1.

Tulislah bentuk sederhana dari bilangan di bawah ini:

2x²– 3x – 9 / 4x² – 9 ?

Jawab:

Pemfaktoran dari pembilang nya yaitu:

2x² – 3x – 9 = 2x² – 6x + 3x – 9

= 2x ( x – 3 ) + 3 ( x -3 )

= ( 2x + 3 ) ( x – 3 )

Pemfaktoran dari penyebut nya yaitu:

4x² – 9 = ( 2x – 3 ) ( 2x + 3 )

Sehingga akan kita dapatkan:

2x² – 3x – 9 / 4x² – 9 = ( 2x + 3 ) ( x – 3 ) / ( 2x – 3 ) ( 2x +3 )

Lalu hilangkan faktor yang memiliki nilai sama antara pembilang dan penyebut nya, yaitu 2x + 3. Maka akan kita dapatkan hasil akhir seperti berikut ini:

2x² – 3x – 9 / 4x² – 9 = x -3 / 2x – 3

Sehingga, hasil bentuk sederhana dari bilangan

2x²– 3x – 9 / 4x² – 9 adalah x -3 / 2x – 3.

Soal 2.

Berapakah hasil dari bilangan aljabar berikut ini: 2 ( 4x – 5 ) − 5x + 7 ?

Jawab:

2 ( 4x 5 ) 5x + 7 = 8x -10 – 5x + 7

= 8x – 5x – 10 + 7

= 3x – 3

Sehingga, hasil dari bilangan

2 ( 4x – 5 ) − 5x + 7 adalah 3x – 3.

Soal 3.

Berapakah hasil dari bilangan aljabar berikut ini ( 2x – 2 ) ( x + 5 ) ?

Jawab:

( 2x – 2 ) ( x + 5 ) = 2x ( x + 5 ) – 2 ( x + 5 )

= 2x ² + 10x – 2x – 10

= 2x ² + 8x – 10

Sehingga, hasil dari bilangan ( 2x – 2 ) ( x + 5 ) adalah

2x ² + 8x – 10.

Soal 4.

Berapakah hasil dari bilangan aljabar berikut ini: 2 / 3x + 3x + 2 / 9x ?

Jawab:

2 / 3x + 3x + 2 / 9x = 2 . 9x + ( 3x + 2 ) . 3x

= 18x + 9x² + 6x / 3x . 9x

= 9x² + 24x / 3x . 9x

= 3x ( 3x + 8 ) / 3x . 9x

Lalu kita hilangkan faktor yang sama antara pembilang serta penyebut nya. Sehingga akan kita dapatkan hasilnya menjadi:

2 / 3x + 3x + 2 / 9x = 3x + 8 / 9x

Sehingga, hasil dari bilangan 2 / 3x + 3x + 2 / 9x adalah

3x + 8 / 9x.

Soal 5.

Tulislah bentuk sederhana dari bilangan aljabar berikut ini: 3x² – 13x – 10 / 9x² – 4 ?

Jawab:

Pemfaktoran dari pembilang nya adalah:

3x² – 13x – 10 = 3x² – 15x + 2x – 10

= 3x ( x – 5 ) + 2 ( x – 5 )

= ( 3x + 2 ) ( x – 5 )

Pemfaktoran dari penyebut nya adalah:

9x² – 4 = ( 3x + 2 ) ( 3x – 2 )

Sehingga akan kita dapatkan:

3x² – 13x – 10 / 9x² – 4 = ( 3x + 2 ) ( x – 5 ) / ( 3x + 2 ) ( 3x – 2 )

Lalu kita hilangkan faktor yang sama antara pembilang serta penyebut nya yaitu 3x + 2. Sehingga akan kita dapatkan hasilnya menjadi:

3x² – 13x – 10 / 9x² – 4 = x – 5 / 3x – 2

Sehingga, hasil bentuk sederhana dari bilangan 3x² – 13x – 10 / 9x² – 4 adalah

x – 5 / 3x – 2.

Soal 6.

Berapakah hasil dari bilangan aljabar berikut ini ( 2x – 2 ) ( x + 5 ) ?

Jawab:

( 2x – 2 ) ( x + 5 ) = 2x ( x + 5 ) – 2 ( x + 5 )

= 2x² + 10x – 2x – 10

= 2x² + 8x – 10

Sehingga, hasil dari bilangan ( 2x – 2 ) ( x + 5 ) adalah

2x² + 8x – 10.

Soal 7.

Kurangilah bilangan berikut ini: 9a – 3 dari 13a + 7 ?

Jawab:

( 13a + 7 ) – ( 9a – 3 ) = 13a + 7 – 9a + 3

= 13a – 9a + 7 + 3

= 4a + 10

Sehingga, hasil pengurangan dari bilangan 9a – 3 dari 13a + 7 adalah

4a + 10.

Soal 8.

Berapakah hasil dari bilangan aljabar berikut ini: ( 2x – 4 ) ( 3x + 5 ) ?

Jawab:

( 2x – 4 ) ( 3x + 5 ) = 2x ( 3x + 5 ) – 4 ( 3x + 5 )

= 6x² + 10x – 12x – 20

= 6x² – 2x – 20

Sehingga, hasil dari bilangan ( 2x – 4 ) ( 3x + 5 ) adalah

6x² – 2x – 20.

Soal 9.

Berapakah hasil pemfaktoran dari bilangan 4x² – 9y² ?

Jawab:

Harus kalian ingat bahwa bentuk faktor nya adalah aljabar seperti:

a² – b² = ( a + b ) ( a – b )

4x² = ( 2x )²

9y² = ( 3y )²

Sehingga faktor dari bilangan 4x² – 9y² adalah

4x² – 9y² = ( 2x + 3y ) ( 2x – 3y )

Sehingga, hasil pemfaktoran dari bilangan 4x² – 9y² adalah

( 2x + 3y ) ( 2x – 3y ).

Soal 10.

Berapakah hasil dari bilangan aljabar berikut ini: ( 2a – b ) ( 2a + b ) ?

Jawab:

( 2ab ) ( 2a + b ) = 2a ( 2a + b ) – b ( 2a + b )

= 4a² + 2ab – 2ab – b²

= 4a² – b²

Sehingga, hasil dari bilangan ( 2a – b ) ( 2a + b ) adalah

4a² – b².

Soal 11.

Berapakah hasil pemfaktoran dari bilangan aljabar berikut ini: 16x² − 9y² ?

Jawab:

Harus kalian ingat bahwa bentuk faktor nya adalah aljabar seperti:

a² – b² = ( a + b ) ( a – b )
16x² = ( 4x )²
9y² = ( 3y )²

Sehingga faktor dari bilangan 4x² – 9y² adalah:

16x² – 9y² = ( 4x + 3y ) ( 4x – 3y )

Maka dari itu, hasil pemfaktoran dari bilangan 16x² − 9y² adalah

( 4x + 3y ) ( 4x – 3y ).

Baca juga: Turunan Fungsi Aljabar

Demikianlah ulasan singkat mengenai Pengenalan Variabel yang dapat kami sampaikan. Semoga ulasan di atas mengenai Pengenalan Variabel dapat kalian jadikan sebagai bahan belajar kalian.

The post Pengenalan Variabel appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Pengenalan Variabel (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.