Uraian: Pola Bilangan (Lengkap)

Pola Bilangan - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Pola Bilangan?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Pola Bilangan ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Pola Bilangan

Pola bilangan matematika merupakan suatu susunan dari beberapa angka yang bisa membentuk pola tertentu.

Pernahkah kalian memperhatian sebuah dadu? Di mana pada setiap dadu memiliki titik-titik bulat yang disebut noktah atau titik pada setiap sisinya.

Pemakain noktah tersebut sebetulnya telah dipakai sejak pada zaman dahulu. Dan uniknya lagi, ternyata noktah tersebut juga didasarkan pada bentuk bangun datar atau bangun ruang.

Seluruh bilangan asli bisa kita gambarkan dengan pemakaian noktah yang mengikuti pola garis lurus.

Jenis-jenis Pola Bilangan

Berikut akan kami beirkan penjelasan lebih rinci dari masing-msaing jenis pola bilangan di dalam matematika. Diantaranya yaitu:

1. Pola Bilangan Garis Lurus

Penulisan bilangan yang mengikuti pola garis lurus adalah suatu pola bilangan yang paling sederhana dibandingkan dengan pola bilangan yang lainnya.

Sebuah bilangan hanya digambarkan dengan menggunakan noktah dengan mengikuti pola garis lurus.

Sebagai contoh:

a. ●●              : mewakitil bilangan dua.

b. ●●●           : mewakili bilangan tiga.

c. ●●●●         : mewakiliki bilangan empat.

d. ●●●●●      : mewakili bilangan lima.

Contoh Pola Bilangan Garis Lurus

Gambarkan bilangan-bilangan berikut dalam bentuk noktah dengan pola garis!

a. 7

b. 9

c. 10

Jawab:

a. ●●●●●●●

b. ●●●●●●●●●

c. ●●●●●●●●●●

2. Pola Bilangan Persegi Panjang

Pada umumnya, penulisan pada bilangan yang dilandasi dengan pola persegipanjang hanya dipakai dalam bilangan yang bukan bilangan prima.

Pada pola ini, noktah-noktah disusun akan menyerupai bentuk persegipanjang.

Sebagai contoh:

a.
●●●●●
●●●●●

noktah di atas mewakili bilangan 10, yakni 2 x 5 = 10

b.
●●●
●●●

noktah di atas mewakili bilangan 6, yakni 2 x 3 = 6

c.
●●
●●
●●

noktah di atas mewakili bilangan 6, yakni 3 x 2 = 6

Contoh Pola Bilangan Persegi panjang

Dari bilangan-bilangan berikut, manakah yang bisa mengikuti pola persegipanjang? Jelaskan dengan menggunakan gambar!

a. 15

b. 16

c. 17

Jawab:

a. Bilangan 15 adalah hasil dari perkalian antara 3 dan 5, sehingga,

●●●●●
●●●●●
●●●●●

pola di atas mengikuti pola persegi panjang.

b. Bilangan 16 adalah hasil dari perkalian antara 2 dan 8, sehingga,

●●●●●●●●
●●●●●●●●

noktah di atas mengikuti pola persegi panjang.

c. Bilangan 17 adalah hasil dari perkalian 1 dan 17, sehingga,

●●●●●●●●●●●●●●●●●

noktah di atas mengikuti pola garis lurus.

3. Pola Bilangan Persegi

Persegi adalah suatu bangun datar yang seluruh sisinya memiliki ukuran yang sama panjang.

Begitu juga dengan penulisan pola bilangan yang mengikuti pola persegi.

Seluruh noktah akan digambarkan dengan menggunakan jumlah yang sama.

Perhatikan penjelasan di bawah ini!

a. ● mewakili bilangan 1, yakni 1 x 1 = 1

b.

●●
●● mewakili bilangan empat, yakni 2 x 2 = 4

c.

● ● ●
● ● ●
● ● ● mewakili bilangan semibilan, yakni 3 x 3 = 9

d.

●●●●
●●●●
●●●●
●●●● mewakili bilangan enam belas, yakni 4 x 4 = 16

Apabila kita lanjutkan, maka bilangan-bilangan yang digambarkan untuk mengikuti pola persegi diantaranya yaitu: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …

Bilangan-bilangan tersebut adalah bilangan kuadrat (pangkat dua). Apabila kalian perhatikan, bilangan kuadrat mempunyai  pola sebagai berikut.

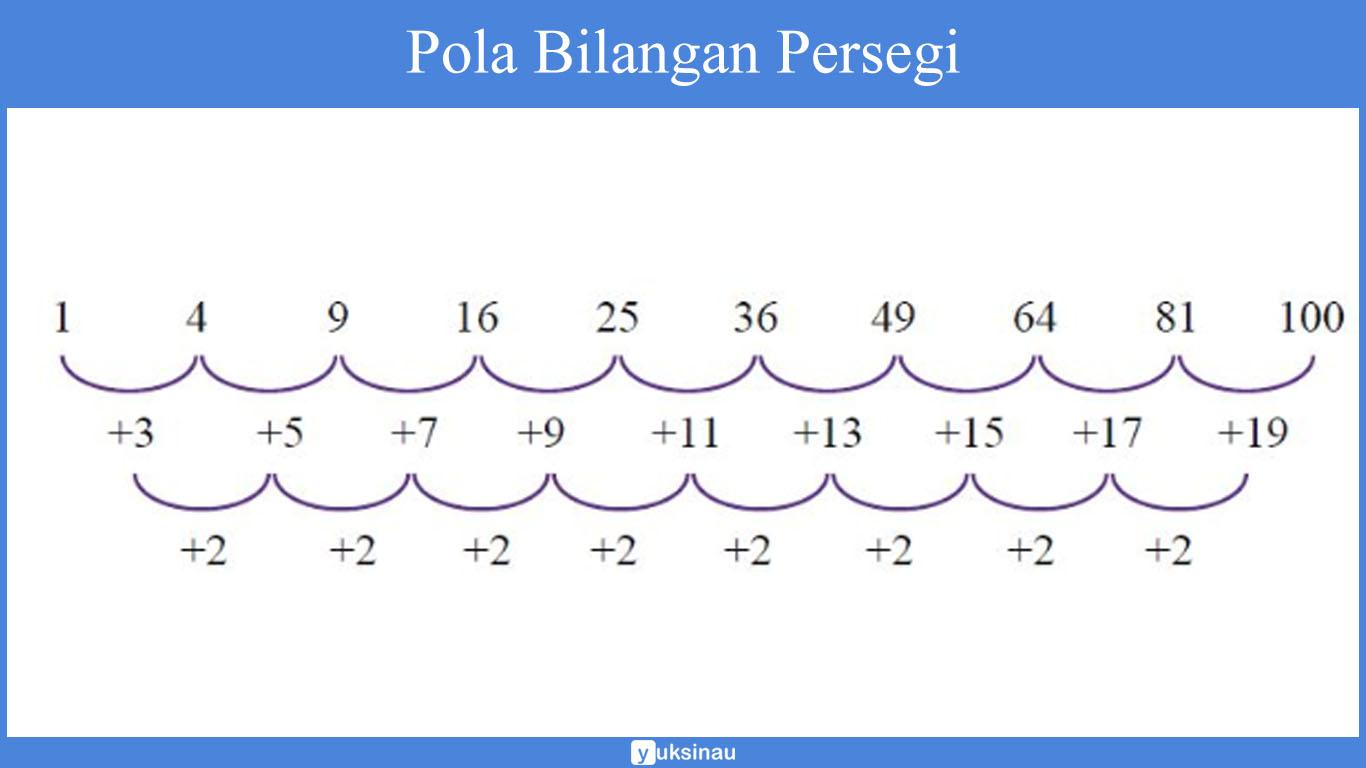
4. Pola Bilangan Segitiga

Selain mengikuti pola persegipanjang dan juga persegi, bilangan juga bisa kita gambarkan dengan menggunakan noktah yang mengikuti pola segitiga.

Untuk lebih jelasnya, coba kalian perhatikan kelima bilangan yang mengikuti pola segitiga di bawah ini:

a. ● mewakili bilangan 1

b.
●
●● mewakili bilangan 3

c.

●
●●
●●● mewakili bilangan 6

d.

●
●●
●●●
●●●● mewakili bilangan 10

Sehingga, bilangan yang mengikuti pola segitiga bisa kita tuliskan seperti berikut ini:

1, 3, 6, 10, 15, 21, 28, 36, 45, …

Coba kalian perhatikan bilangan yang mempunyai pola segitiga. Ternyata, bilangan-bilangan tersebut dibentuk dengan mengikuti pola sebagai berikut.

atau

1   = 1

3   = 1+2

6   = 1+2+3

10 = 1 + 2 + 3 + 4

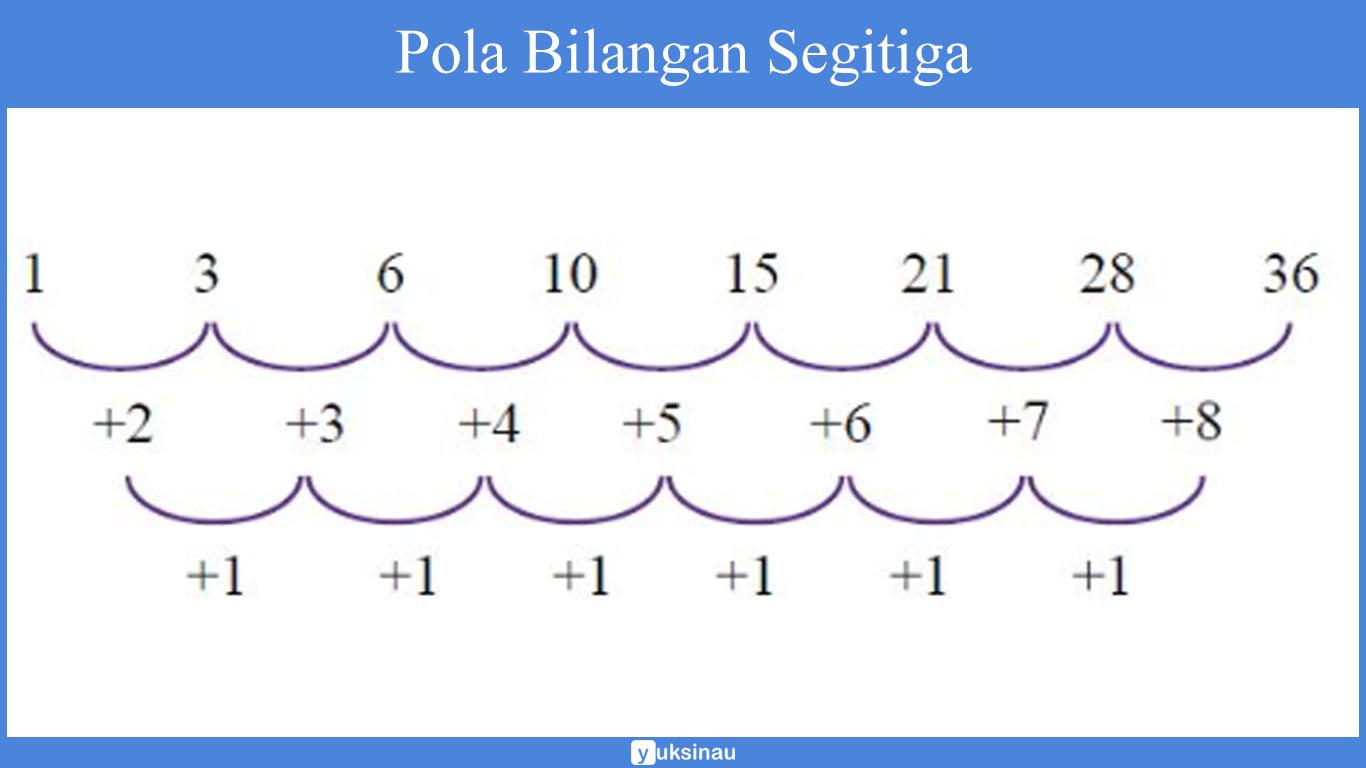
15 = 1 + 2 + 3 + 4 + 5 dan begitu seterusnya.

Apa yang bisa kalian simpulkan dari uraian di atas? Tulis di kolom komentar ya…

5. Pola Bilangan Ganjil dan Genap

Bilangan yang mempunyai pola bilangan ganjil atau genap pada umumnya mempunyai selisih dua angka antara bilangan yang satu dengan bilangan sebelumnya.

Informasi selengkapnya perhatikan uraian di bawah ini.

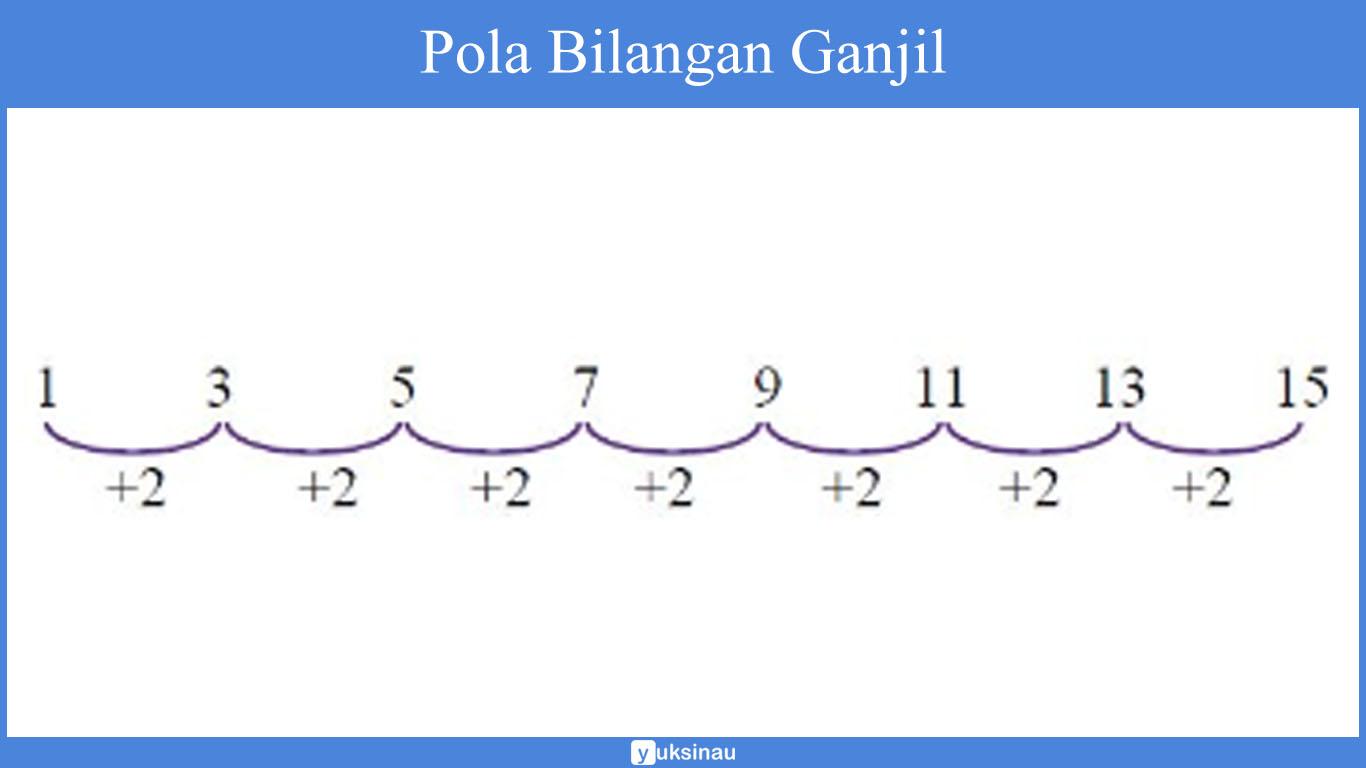
a. Pola Bilangan Ganjil

Pola bilangan ganjil mempunyai dua aturan seperti beriktu ini:

1. Bilangan 1 sebagai bilangan awal.
2. Bilangan selanjutnya mempunyai silisih 2 dengan bilangan sebelumnya.

Perhatikan pola bilangan ganjil di bawah ini:

b. Pola Bilangan Genap

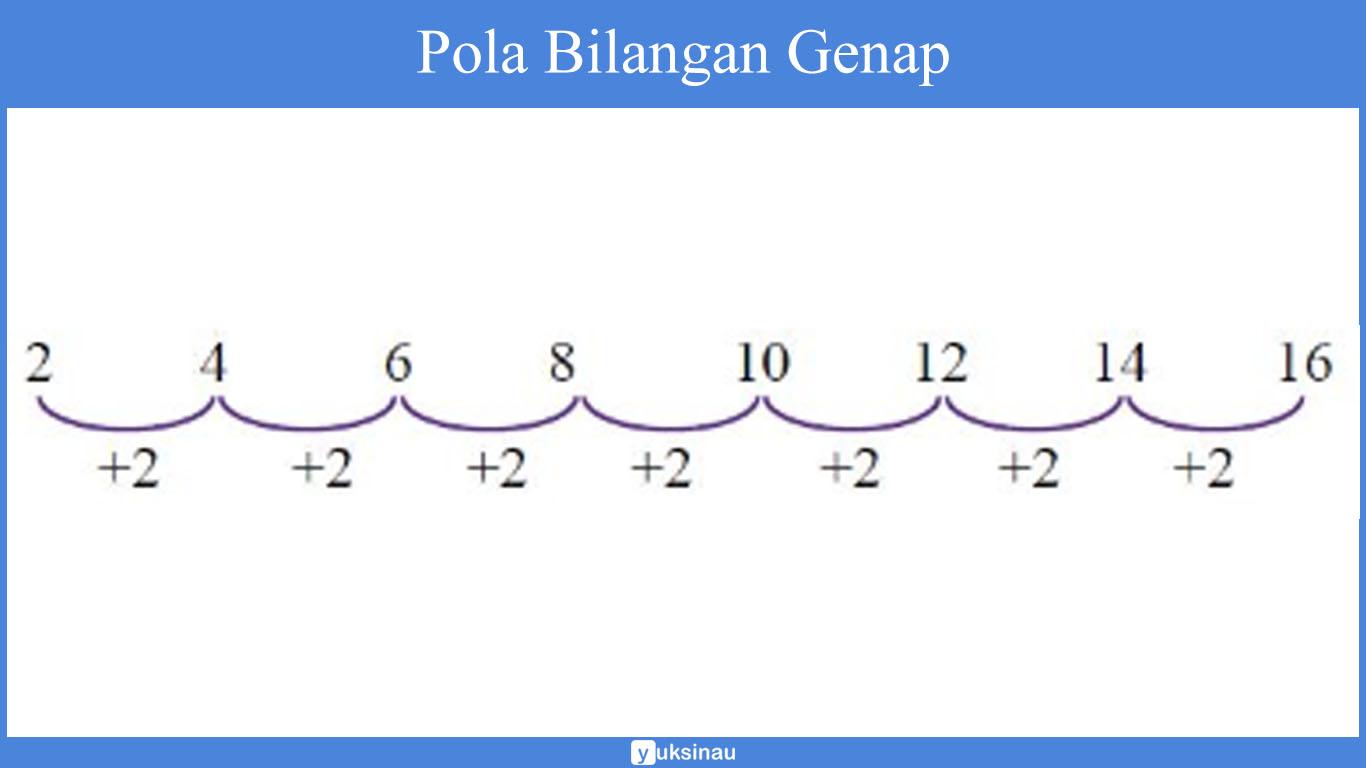
Pola bilangan genap mempunyai dua aturan seperti berikut ini:

1. Bilangan 2 sebagai bilangan awal.
2. Bilangan selanjutnya memiliki selisih 2 dengan bilangan sebelumnya.

Perhatikan pola bilangan genap di bawah ini:

6. Pola Segitiga Pascal

Bilangan-bilangan yang disusun memakai pola segitiga Pascal ini mempunya pola yang unik daripada pola-pola sebelumnya.

Hal tersebut dikarenakan pada bilangan yang berpola segitiga Pascal selalu diawali dan juga diakhiri oleh angka 1. Tak hanya itu saja, pada susunannya juga selalu ada angka yang diulang.

Adapun beberapa aturan untuk membuat pola segitiga Pascal, diantaranya adalah sebagai berikut:

1. Angka 1 adalah angka awal yang ada di puncak.
2. Simpan dua bilangan di bawahnya. Oleh sebab itu, angka awal dan akhir selalu angka 1, kedua bilangan tersebut yaitu 1.
3. Berikutnya, jumlahkan bilangan yang berdampingan. Lalu, simpan hasilnya di bagian tengah bawah kedua bilangan tersebut.
4. Proses ini dilakukan terus hingga batas susunan bilangan yang diminta.

Untuk lebih jelasnya, perhatikan pola segitiga Pascal di bawah ini:

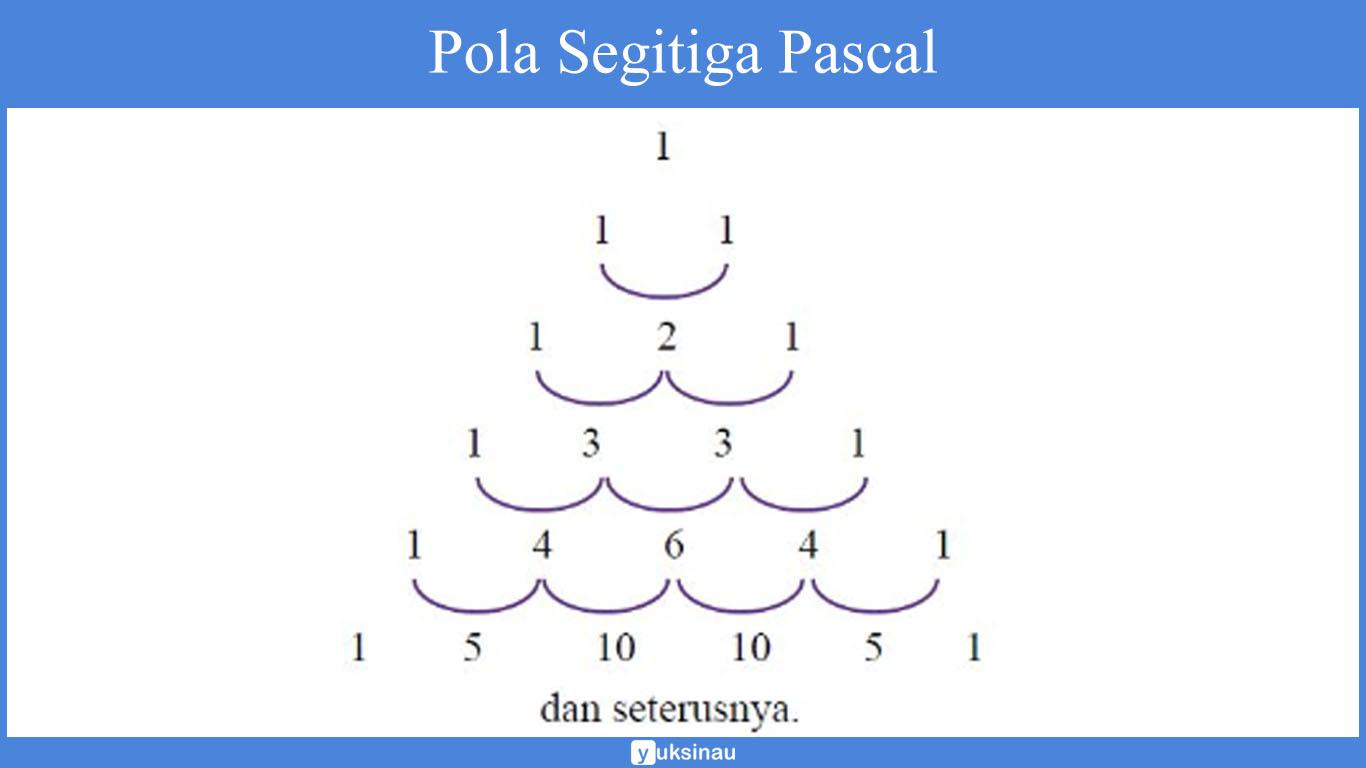
Suku-suku yang ada pada pola bilangan pascal ternyata sama dengan suku-suku pada barisan bilangan kelipatan dua.

Suku berikutnya dapat kalian cari dengan mencari hasil hasil kali dua dengan suku sebelumnya.

Contoh Soal dan Pembahasan

Contoh Soal Pola Bilangan Persegi

Soal 1.

Dengan memakai ciri-ciri penulisan bilangan yang mempunyai pola persegi, tentukan bilangan manakah yang mengikuti pola persegi?

1. 60
2. 196
2. 225

Soal 2.

Seorang anak menyusun persegi dari batang lidi dengan mengikuti pola sebagai berikut.

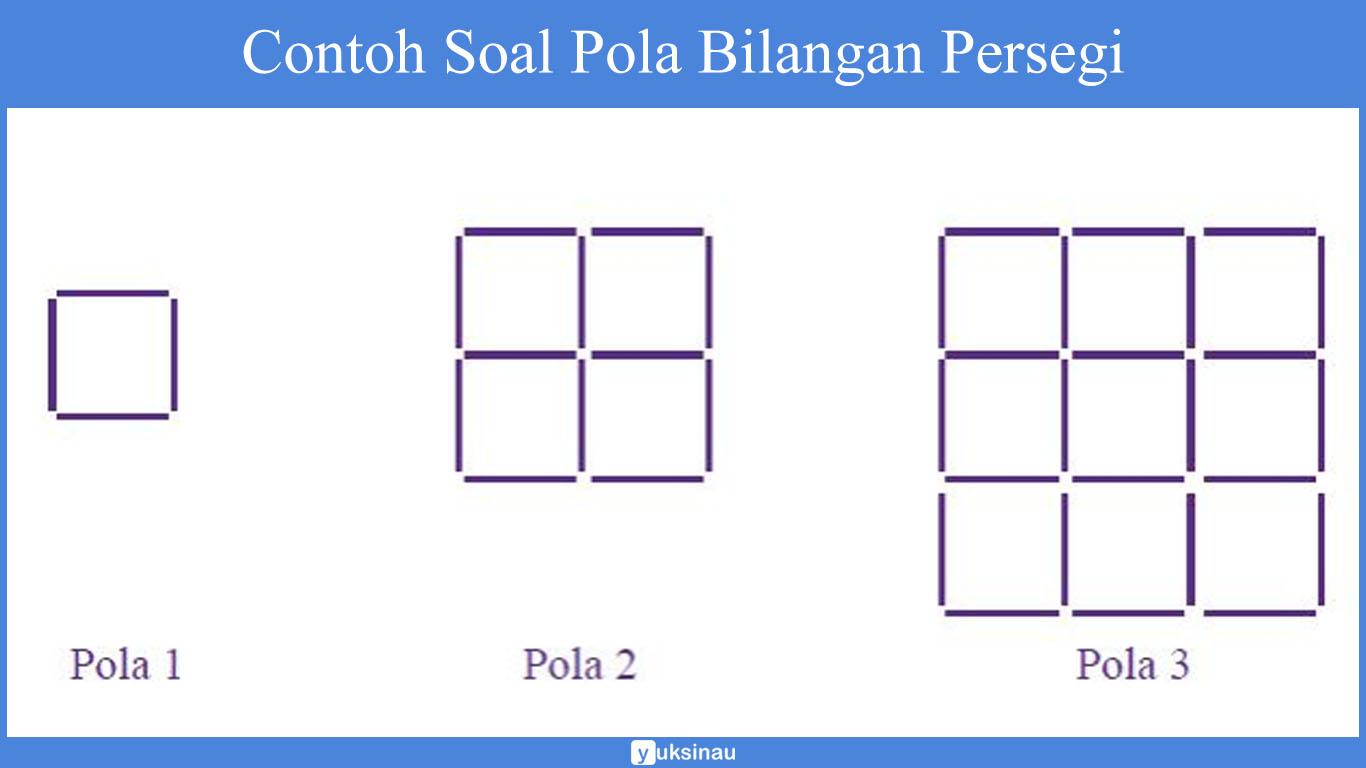
Berapa banyak lidi yang diperlukan guna membuat persegi pada pola ke-5?

Jawab:

Soal 1.

Yang termasuk pada pola bilalngan persegi yaitu;

1. Bilangan 60 bukan merupakan bilangan kuadrat. Sehingga, bilangan 60 tidak bisa kita gambarkan dengan mengikuti pola persegi.
2. Bilangan 196 adalah bilangan kuadrat dari 14. Sehingga, bilangan 196 bisa kita gambarkan dengan mengikuti pola persegi.
3. Bilangan 225 adalah bilangan kuadrat dari 15. Sehingga, bilangan 225 bisa kita gambarkan dengan mengikuti pola persegi.

Soal 2.

Persegi yang dapat dibentuk pada pola ke-5 bisa kita gambarkan seperti berikut ini:

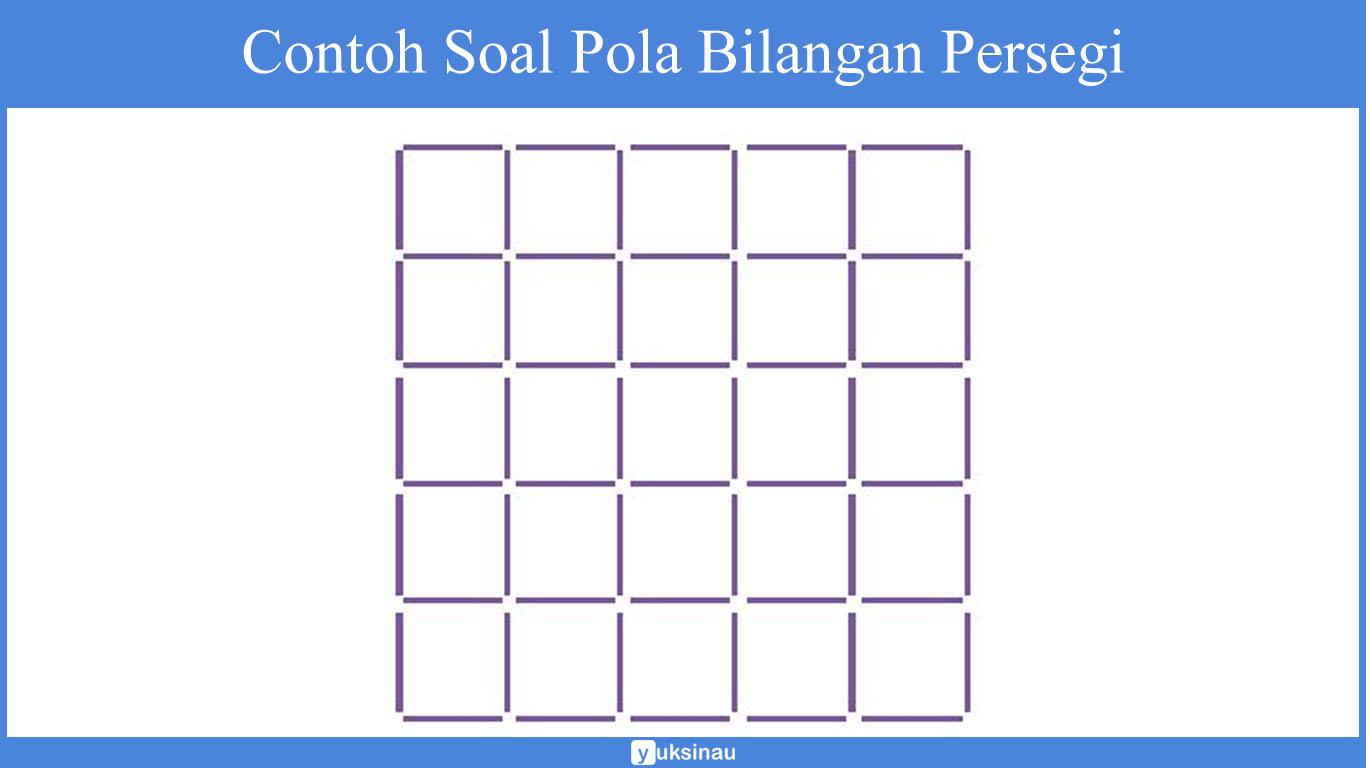
Dari gambar di atas, banyak lidi yang diperlukan untuk membuat persegi pada pola ke-5 yaitu sebanyak 60 lidi.

Contoh Soal Pola Bilangan Segitiga

Soal 1.

Tentukan lima bilangan segitiga setelah bilangan 36.

Soal 2.

Seorang anak membuat kerangka segitiga dari batang lidi dengan mengikuti pola seperti berikut ini:

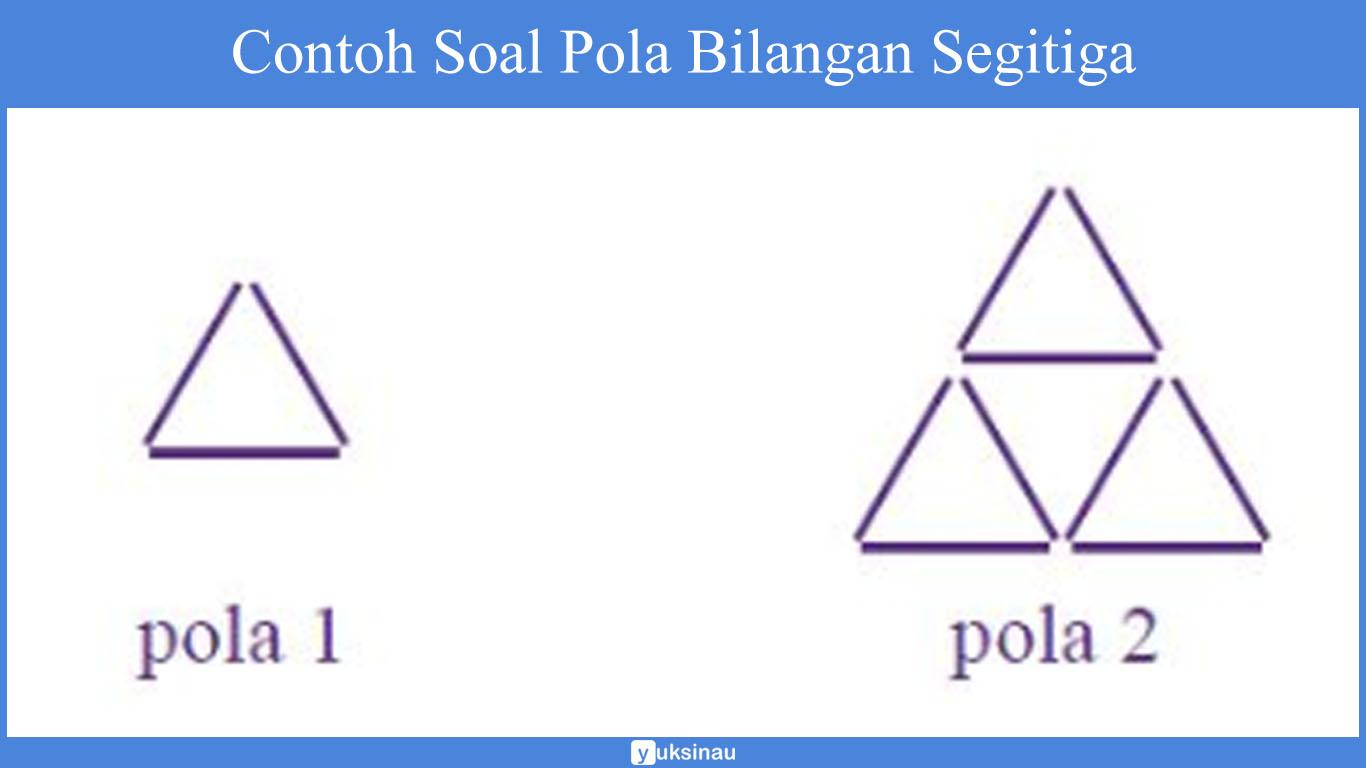
Berapa banyak lidi yang dibutuhkan untuk membuat pola ke-4?

Jawab:

Soal 1.

Lima bilangan segitiga sesudah bilangan 36 bisa kita tentukan dengan menggunakan pola di bawah ini:

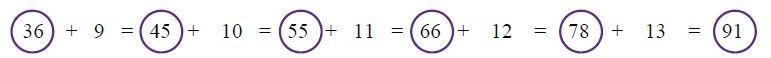
Sehingga, bilangan segitiga tersebut yaitu 45, 55, 66, 78 dan 91

Soal 2.

Segitiga yang dibentuk pada pola keempat bisa ita gambarkan seperti di bawah ini:

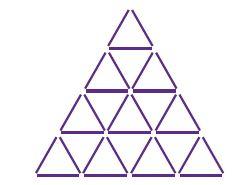
Dari gambar di atas, banyaknya batang lidi yang diperlukan dalam membuat kerangka segitiga yang sesuai dengan pola ke-4 yaitu sebanyak 30 batang lidi.

Contoh Soal Pola Bilangan Genap dan Ganjil

Soal 1.

Isilah titik-titik di bawah ini sehingga membentuk pola bilangan genap.

… … … … 28 … … … … 38 …

Soal 2.

Isilah titik-titik di bawah ini sehingga membentuk pola bilangan ganjil.

… 51 … … … … … … … … … 69

Jawab:

Soal 1.

Pola bilangan genap yang dimaksud yaitu

20 22 24 26 28 30 32 34 36 38 40

Soal 2.

Pola bilangan ganjil yang dimaksud yaitu

49 51 53 55 57 59 61 63 65 67 69

Baca juga: Penyajian Data dalam Diagram

Demikianlah ulasan singkat kali ini mengenai pola bilangan matematika yang dapat kami sampaikan. Semoga ulasan di atas mengenai pola bilangan matematika yang dapat kalian jadikan sebagai bahan belajar kalian.

The post Pola Bilangan appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Pola Bilangan (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.