Uraian: Belah Ketupat (Lengkap)

Belah Ketupat - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Belah Ketupat?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Belah Ketupat ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Belah Ketupat

Seperti yang telah kita ketahui, salah satu sifat pada belah ketupat juga dimiliki oleh sifat persegi, yakni seluruh / keempat sisinya sama panjang. Maka dari itu, untuk mencari keliling belah ketupat dapat kalian cari dengan menggunakan rumus keliling persegi.

Namun, kali ini kami hanya akan membahas secara khusus terkait belah ketupat secara tuntas, simak baik – baik ya.

Pengertian Belah Ketupat

Secara umum, belah ketupat merupakan suatu bangun datar 2 dimensi yang terbentuk oleh 4 buah sisi sama panjang serta memiliki 2 pasang sudut bukan siku – siku dengan sudut yang saling berhadapan memiliki besar yang sama.

Di dalam bahas inggris, bangun ini disebut sebagai “rhombus“.

Sifat Belah Ketupat

Untuk membedakan bangun belah ketupat dengan bangun datar lainnya, maka terdapat beberapa sifat khusus yang melekat, diantaranya yaitu:

1. Besar pada keempat titik sudutnya adalah 360º.

2. Keempat sisinya adalah sama panjang.

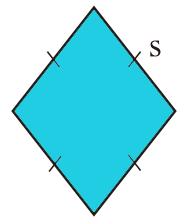
3. Memiliki 2 sumbu simetri yang menjadi diagonalnya.

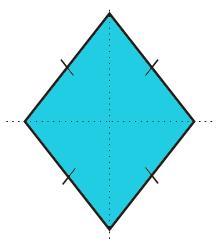
4. Memiliki 2 diagonal yang saling tegak lurus

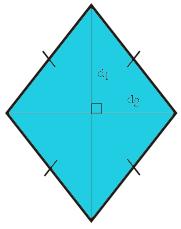
Diagonal 1 (d1) serta diagonal 2 (d2) yang ada pada belah ketupat saling tegak lurus untuk membentuk sudut siku -siku (90°).

5. Sudut yang saling berhadapan memiliki besar yang sama.

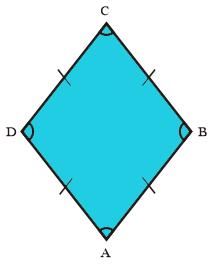
Pada belah ketupat sudut yang berhadapan memiliki besar yang sama. Ilustrasi tersebut menggambarkan bahwa besar sudut ∠ABC = ∠ADC serta ∠BAD = ∠BCD.

Baca juga: Luas Permukaan Kubus

Rumus Belah Ketupat

Berikut adalah rumus yang bisa kalian cari untuk mencari sebuah nilai pada belah ketupat, antara lain:

Nama	Rumus
Keliling (K)	K = s + s + s + s K = s × 4
Luas (L)	L = ½ × d1 × d2
Sisi (s)	s = K ÷ 4
Diagonal 1 (d1)	d1 = 2 × L ÷ d2
Diagonal 2 (d2)	d2 = 2 × L ÷ d1

Contoh Soal

Berikut adalah beberapa contoh soal belah ketupat yang dapat kalian pelajari, antara lain:

1. Sebuah bangun belah ketupat mempunyai panjang diagonal 10 cm serta 24 cm. Hitunglah keliling belah ketupat tersebut!

Jawab:

Diketahui:

Panjang diagonal 10 cm serta 24 cm.

Ditanya:

K …?

Penyelesaian:

• Menentukan Panjang Sisi

Kalian dapat memakai konsep Pythagoras, sehingga bisa panjang sisi belah ketupat diketehui:

Panjang sisi = √(52 + 122) = √(25 + 144) = √169 = 13 cm

• Keliling

K = 4 x s
= 4 x 13 cm
= 52 cm.

Sehingga diketahui kelilingnya adalah 52 cm.

2. Sebidang tanah yang bentuknya belah ketupat memiliki panjang diagonal – diagonalnya ialah 12 cm dan 10 cm. Berapakah luas tanah tersebut?

Jawab:

Diketahui:

Panjang diagonal 12 cm dan 10 cm.

Ditanya:

L …?

Penyelesaian:

L = ½ x d1 x d2
L = ½ x 12 cm x 10 cm
L = ½ x 120 cm²
L = 60 cm²

Sehingga diketahui luasnya adalah 60 cm²

3. Sebuah bangun belah ketupat mempunyai sisi – sisi yang berukuran 30 cm. Hitunglah keliling bangun belah ketupat tersebut!

Jawab:

Diketahui:

Sisi = 30 cm

Ditanya:

K …?

Penyelesaian:

K = 4 x s
K = 4 x 30 cm
K = 120 cm

Sehingga diketahui kelilingnya adalah 120 cm.

4. Suatu belah ketupat memiliki keliling 20 cm. Hitunglah panjang sisi belah ketupat tersebut!

Jawab:

Diketahui:

K = 20 cm

Ditanya:

s …?

Penyelesaian:

K = 4 × s
s = Kll ÷ 4
s = 20 cm ÷ 4
s = 5 cm

Sehingga dapat diketahui sisinya yaitu 5 cm.

5. Hitunglah suatu belah ketupat yang mempunyai panjang sisi 7 cm!

Jawab:

Diketahui:

s = 7 cm

Ditanya:

K …?

Penyelesaian:

K = 4 × s
K = 4 x 7 cm
K = 28 cm

Sehingga diketahui kelilingnya adalah 28 cm.

6. Sebuah belah ketupat memiliki luas 24 cm². Jika diketahui salah satu diagonalnya memiliki ukuran 4 cm, berapakah panjang diagonal lainnya?

Jawab:

Diketahui:

• L = 24 cm²
• d1 = 4 cm

Ditanya:

d2 ..?

Penyelesaian:

L = ½ × d1 × d2

Dengan memakai konsep aljabar, maka didapatkan:

d2 = 2 × L ÷ d1
d2 = 2 × 24 cm² ÷ 4 cm
d2 = 12 cm

Sehingga diketahui panjang d2 adalah 12 cm.

7. Hitunglah luas belah ketupat yang memiliki panjang diagonal 8 cm serta 7 cm?

Jawab:

Diketahui:

• d1 = 8 cm
• d2 = 7cm

Ditanya:

L …?

Penyelesaian:

L = ½ × d1 × d2
L = ½ x 8 cm × 7 cm
L = 28 cm²

Sehingga diketahui luasnya adalah 28 cm²

8. Terdapat suatu balok yang berbentuk belah ketupat dengan sisi 22 cm. Berapakah keliling belah ketupat tersebut?

Jawab:

Diketahui:

s = 22 cm

Ditanya:

K …?

Penyelesaian:

K = 4 x S
K = 4 x 22 cm
K = 88 cm

Sehingga diketahui kelilingnya adalah 88 cm.

9. Terdapat suatu jendela yang bentuknya belah ketupat dengan sisi 40 cm. Hitunglah keliling sisi jendela tersebut!

Jawab:

Diketahui:

s = 40 cm

Ditanya:

K …?

Penyelesaian:

K = 4 x S
K = 4 x 40
K = 160 cm

Sehingga diketahui keliling jendela tersebut adalah 160 cm.

10. Terdapat sebuah jendela kamar yang bentuknya belah ketupat dengan sisi 8 cm. Berapakah keliling jendela kamar tersebut?

Jawab:

Diketahui:

s = 8 cm

Ditanya:

K …?

Penyelesaian:

K = 4 x S
K = 4 x 8
K = 32 cm

Sehingga diketahui keliling jendela tersebut adalah 32 cm.

The post Belah Ketupat appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Belah Ketupat (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.