Uraian: Persamaan Nilai Mutlak Linier Satu Variabel (Lengkap)
Namun tak ada salahnya sebelum membaca ulasan tentang Persamaan Nilai Mutlak Linier Satu Variabel ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?
Pembahasan Lengkap Persamaan Nilai Mutlak Linier Satu Variabel
Untuk menyelesaikan Persamaan Nilai Mutlak Linier Satu Variabel tidaklah sulit. Tetapi kalian harus paham mengenai konsep nilai mutlak, sifat persamaan serta penyelesaian persamaaan nilai mutlak satu variabel itu sendiri. Berikut informasi selengkapnya untuk kalian.
Pengertian Persamaan Nilai Mutlak Satu Variabel
Di dalam bidang ilmu geometri, nilai mutlak dari x biasa ditulis dengan: | x |, yang merupakan sebuah jarak dari x ke 0 pada garis bilangan real.
Sebab jarak tersebut selalu bernilai positif atau nol, sehingga nilai mutlak x juga akan selalu bernilai positif atau nol untuk masing-masing setiap x bilangan real.
Nilai mutlak merupakan sebuah nilai yang selalu bernilai positif serta biasa dinotasikan seperti: |x|
Secara umum, nilai mutlak ini bisa kita jabarkan menjadi sebagai berikut:
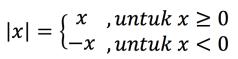
Selain dari persamaan di atas, jika nilai mutlak ada dalam sebuah bentuk aljabar maka bisa kita peroeh sebuah persamaan seperti berikut ini:
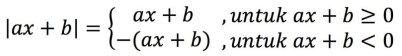
Konsep Nilai Mutlak
Konsep dari nilai mutlak ini, bisa dengan mudah kita pahami dengan memperhatikan contoh di bawah ini:
Seorang pemimpin regu PBB pramuka memerintahkan pasukan untuk maju 4 langkah kedepan, sehingga jarak pergerakan barisan tersebut bergeser sebesar 4 langkah ke arah depan.
Jika pemimpin barisan tersebut kemudian memerintah untuk mundur 3 langkah ke belakang, maka jarak dari perpindahan pergerakan barisan tersebut akan sebesar tiga langkah ke arah belakang.
Besar dari pegerakan barisan di atas merupakan salah satu contoh dari nilai mutlak.
Jika di gambarkan ke dalam bentuk garis bilangan, maka bisa kita lihat menjadi seperti berikut ini:
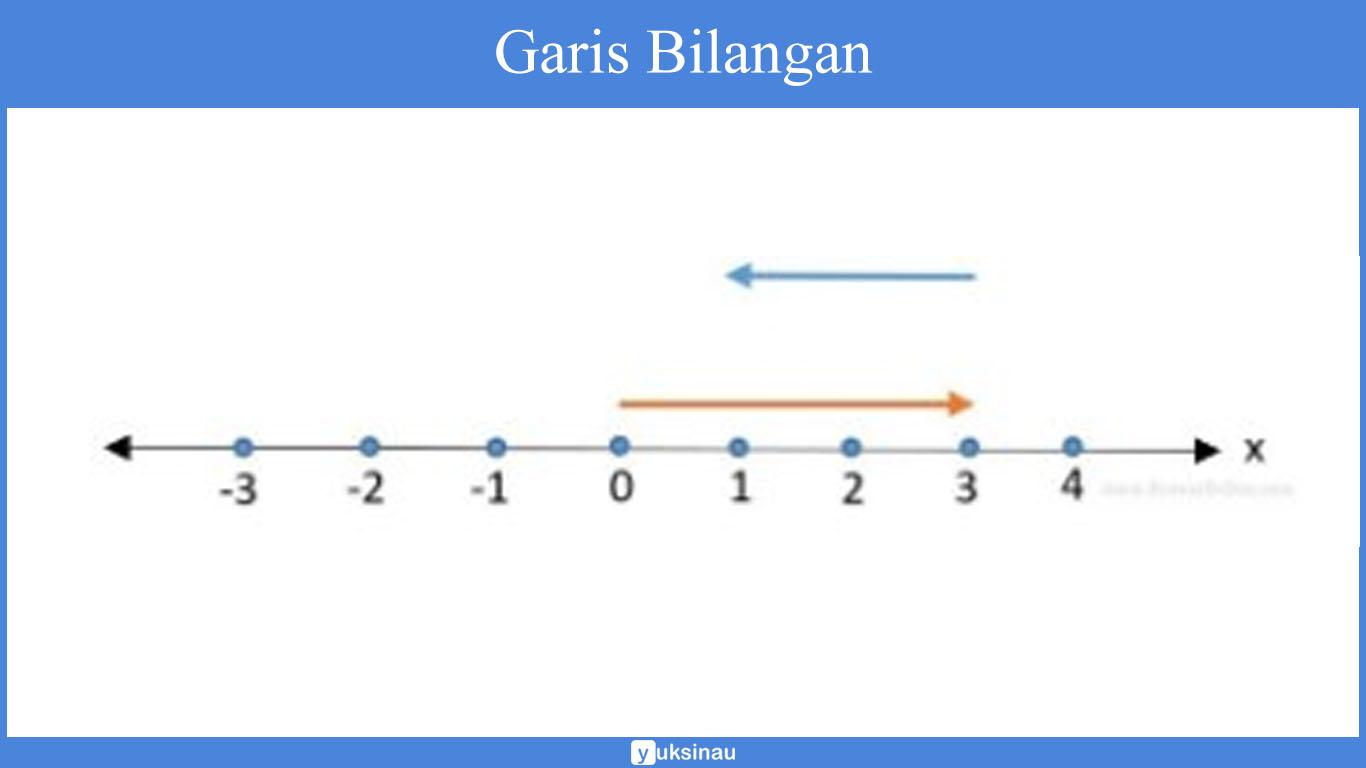
Berdasarkan dari gambar garis bilangan di atas, posisi x =0 merupakan sebuah titik awal barisan.
Lalu, anak panah merah merupakan suatu pergerakan maju 3 langkah ke arah depan (mengarah sumbu x positif atau +3).
Serta untuk anak panah biru merupakan pergeseran mundur 2 langkah ke belakang (mengarah sumbu x negatif atau -2).
Maka dari itu, banyaknya langkah pada barisan tersebut adalah sebuah konsep dari nilai mutlak yakni|3| +|- 2|= 3+2 = 5.
Sifat Persamaan Nilai Mutlak
Nilai mutlak dari sebuah bilangan x bisa juga didefiniskan sebagai jarak bilangan tersebut pada titik 0 pada garis bilangan, dengan tidak memperhatikan arahnya.
Hal tersebut berrarti |x| = 5 mempunyai dua selesaian, sebab terdapat dua bilangan yang jaraknya terhadap 0 adalah 5: x = –5 dan x = 5.
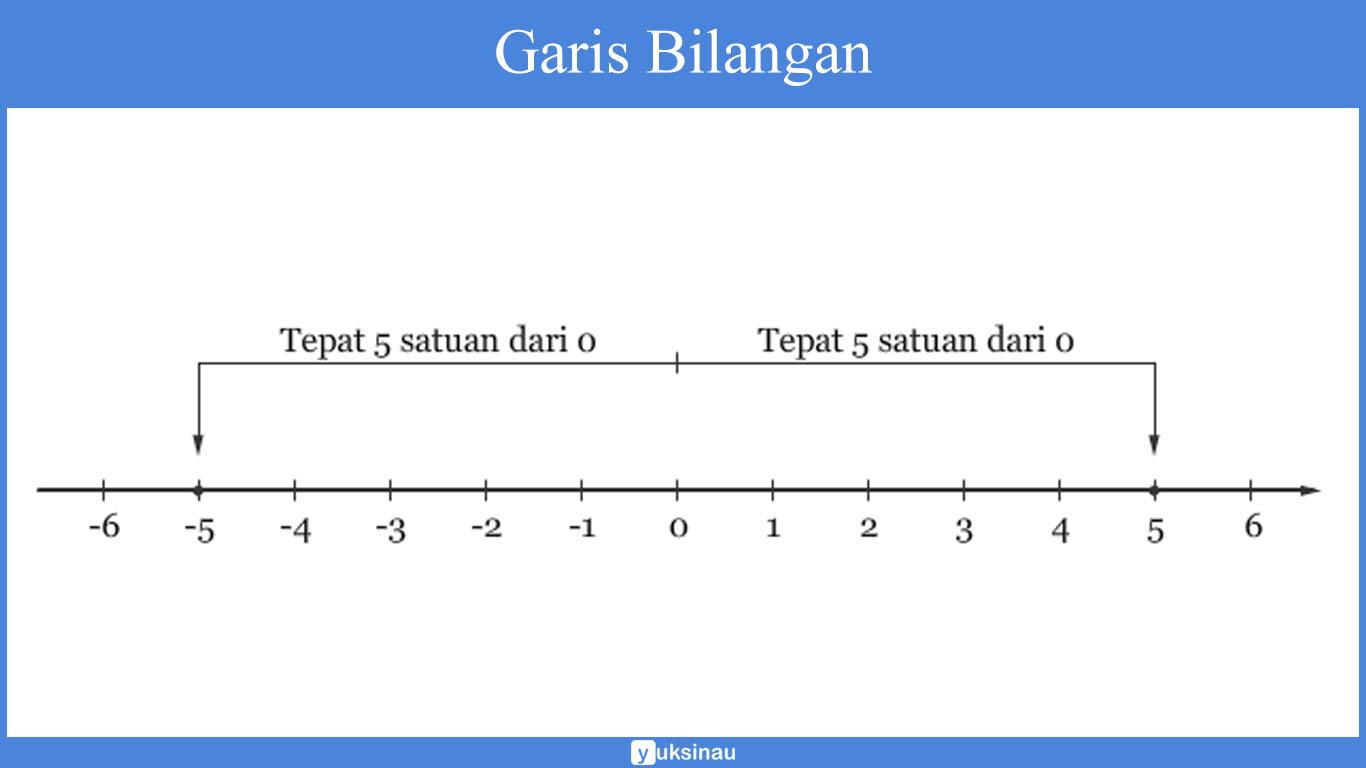
Konsep tersebut bisa juga kita perluas lagi dalam situasi yang melibatkan bentuk – bentuk aljabar yang terletak di dalam simbol nilai mutlak. Seperti yang akan dijabarkan oleh sifat di bawah ini:
- Sifat Persamaan Nilai Mutlak :
Apabila x merupakan sebuah bentuk aljabar dan k merupakan bilangan real positif, maka |X| = k akan mengimplikasikan X = –k atau X = k.
- Sifat Perkalian Nilai Mutlak
Apabila A serta B merupakan bentuk-bentuk aljabar, maka |AB| = |A||B|.
Apabila A = –1 maka menurut sifat tersebut |–B| = |–1||B| = |B|. Secara umum, sifat tersebut akan berlaku untuk sembarang konstanta A.
Persamaan Nilai Mutlak Linear Satu Variabel
Dalam suatu persamaan nilai mutlak linear satu variabel, garis bilangan dipakai sebagai media yang berguna dalam menunjukan nilai mutlak.
Besar dari nilai mutlak tersebut bisa kita lihat dari panjang tanda panah serta dihitung dari nilai nol.
Sementara untuk tanda panah dipakai dalam menentukan suatu besaran dari nilai mutlak, di mana arah ke kiri menunjukan nilai mutlak dari bilangan negatif. Dan begitu pula sebaliknya.
Sementara untuk arah yang ke kanan menunjukan nilai mutlak dari bilangan positif.
Perhatikan baik-baik gambar garis bilangan di bawah ini:
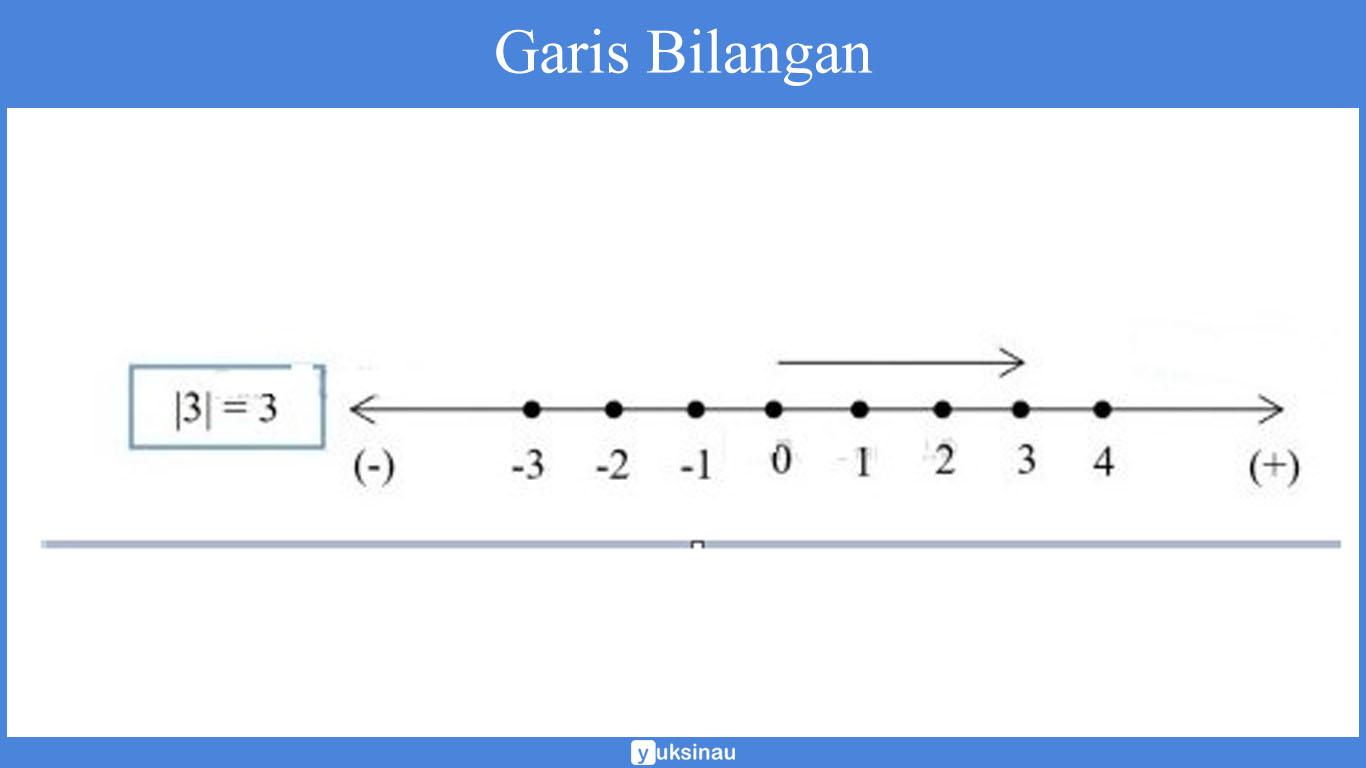
Jika kita lihat pada tanda panah di atas, maka akan kita jumpai pergerakan dari bilangan 0 ke arah kanan menuju bilangan ke 3.
Sehingga besar dari langkah yang dilewati oleh tanda panah di atas yaitu 3 (berjarak 3 satuan dari bilangan 0). Hal ini artinya nilai mutlak tersebut yaitu|3|= 3.
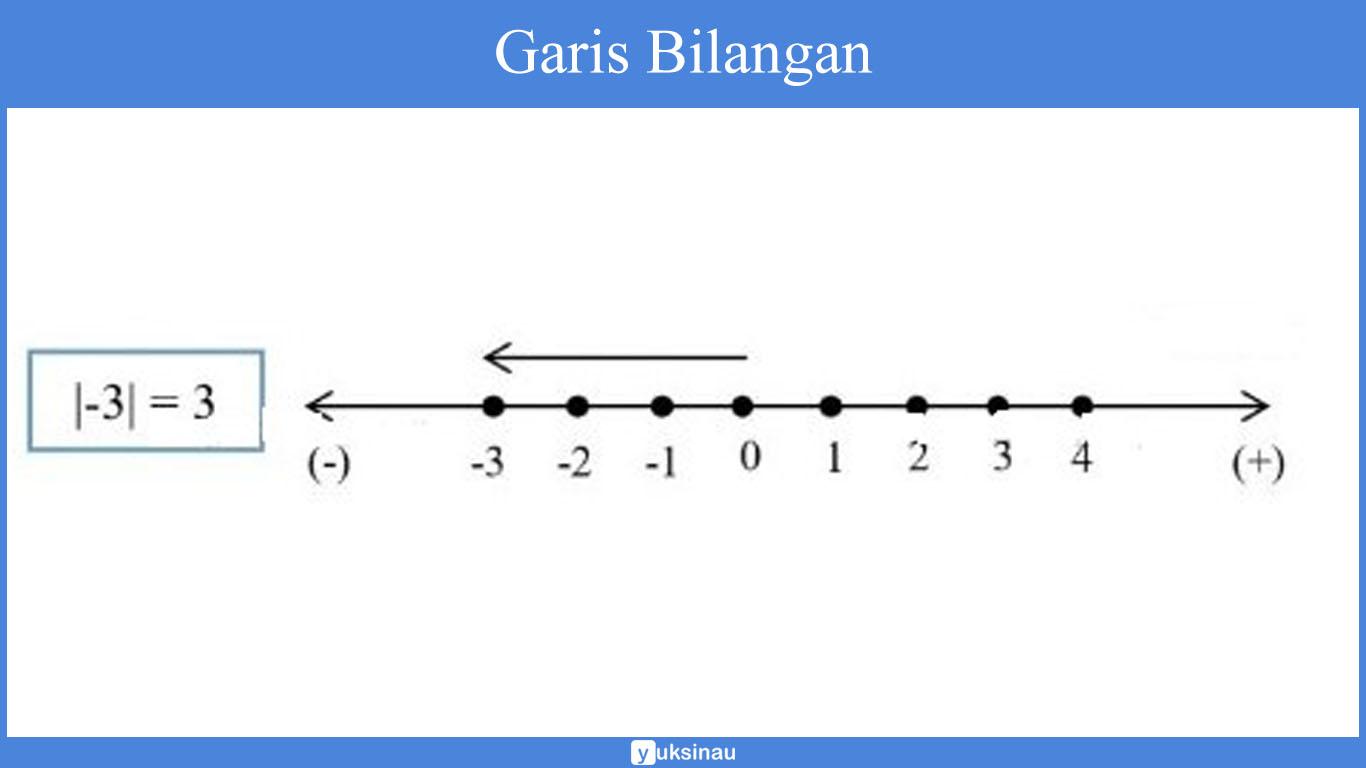
Jika kita lihat pada tanda panah di atas, maka akan kita jumpai pergerakan dari bilangan 0 ke arah kiri menuju bilangan ke 3.
Sehingga besar dari langkah yang dilewati oleh tanda panah di atas yaitu 3 (berjarak 3 satuan dari bilangan 0). Hal ini artinya nilai mutlak tersebut yaitu|-3|= 3.
Berdasarkan dari uraian di atas, nilai mutlak ini bisa juga dikatakan sebagai besaran sebuah jarak perpindahan dari titik awal.
Persamaan dan Pertidaksamaan Nilai Mutlak
Nilai mutlak x merupakan sebuah jarak dari x ke nol dalam garis bilangan real. Dengan artian ini, solusi dari persamaan dan juga pertidaksamaan nilai mutlak dari sebuah bentuk linier akan dapat kita temukan.
Sebagai contoh:
| x | = a dengan a > 0
Persamaan | x | merupakan= a yang berarti jarak dari x ke 0 sama dengan a.
Perhatikan baik-baik gambar garis bilangan di bawah ini:
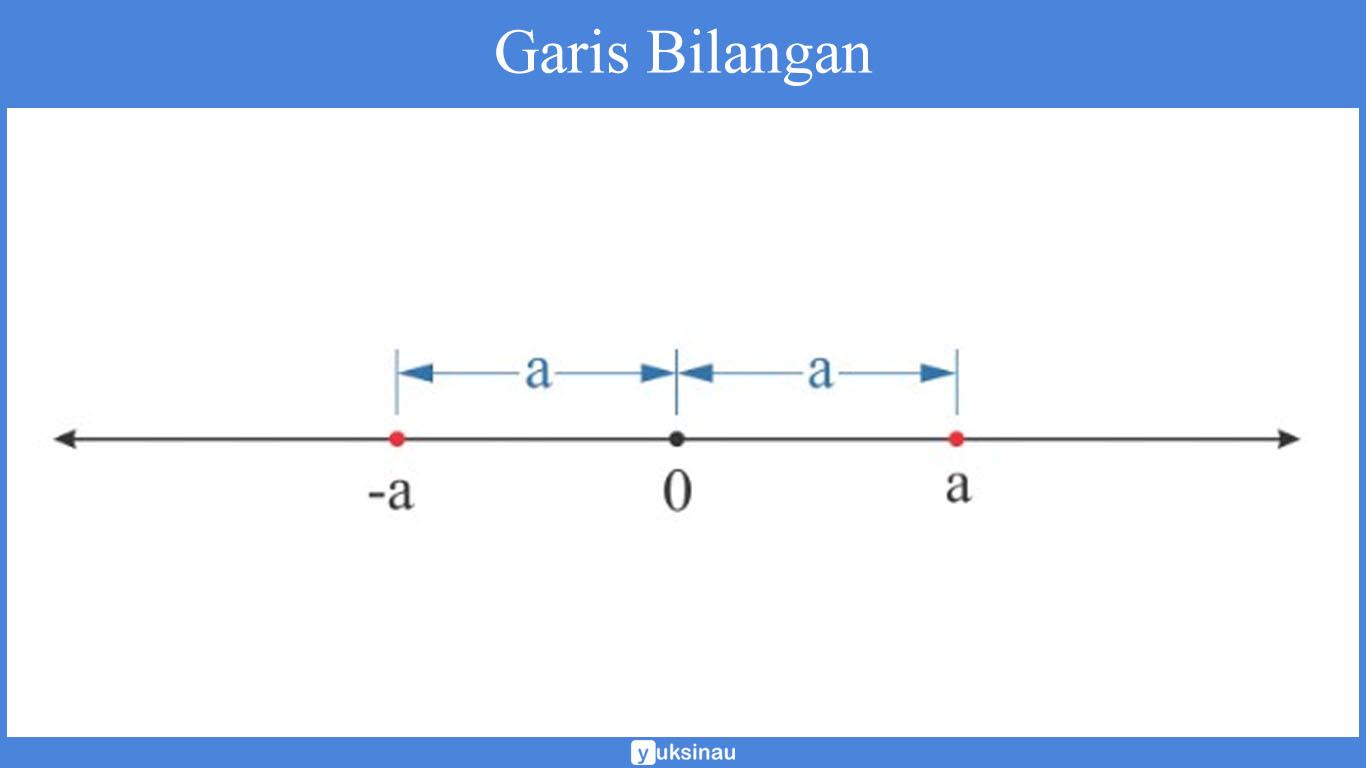
Pada gambar di atas, maka dapat kita simpulkan jika, arah -a ke 0 sama dengan jarak a ke 0, yakni a.
Pertanyaannya yakni dimana x supaya jaraknya ke 0 juga sama dengan a.
Posisi x digambarkan oleh titik merah pada gambar di atas, yang merupakan x = -a atau x = a.
Di mana terlihat bahwa jarak antara titik tersebut ke 0 merupakan sama dengan a. Sehingga, supaya jarak x ke nol sama dengan a, maka haruslah x = -a atau x = a.
| x | < a untuk a > 0
Pertidaksamaan | x | < a, yang mana berarti jarak dari x ke 0 kurang dari a.
Perhatikan baik-baik gambar garis bilangan di bawah ini:
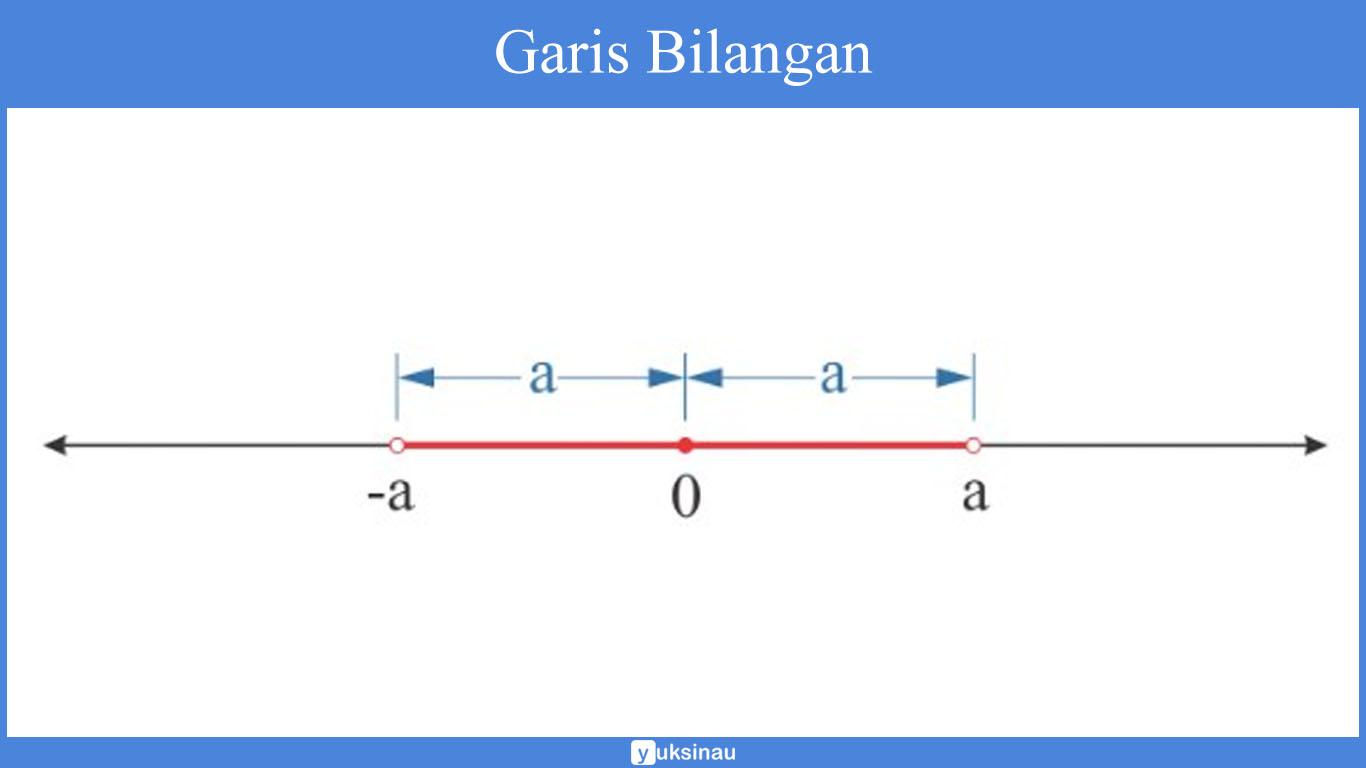
Berdasarkan dari gambar ilustrasi di atas, maka dapat kita ketahui jika posisi x digambarkan oleh ruas garis yang berwarna merah. Yakni himpunan titik-titik diantara -a dengan a yang biasa ditulis -a < x < a.
Jika kemudian kita ambil sebarang titik pada interval tersebut, maka bisa kita pastikan jaraknya ke 0 adalah kurang dari a.
Sehingga, supaya jarak x ke 0 kurang dari a, maka haruslah -a < x < a.
| x | > a untuk a > 0
Pertidaksamaan | x | > a merupakan sebuah jarak dari x ke 0 lebih dari a.
Perhatikan baik-baik gambar garis bilangan di bawah ini:
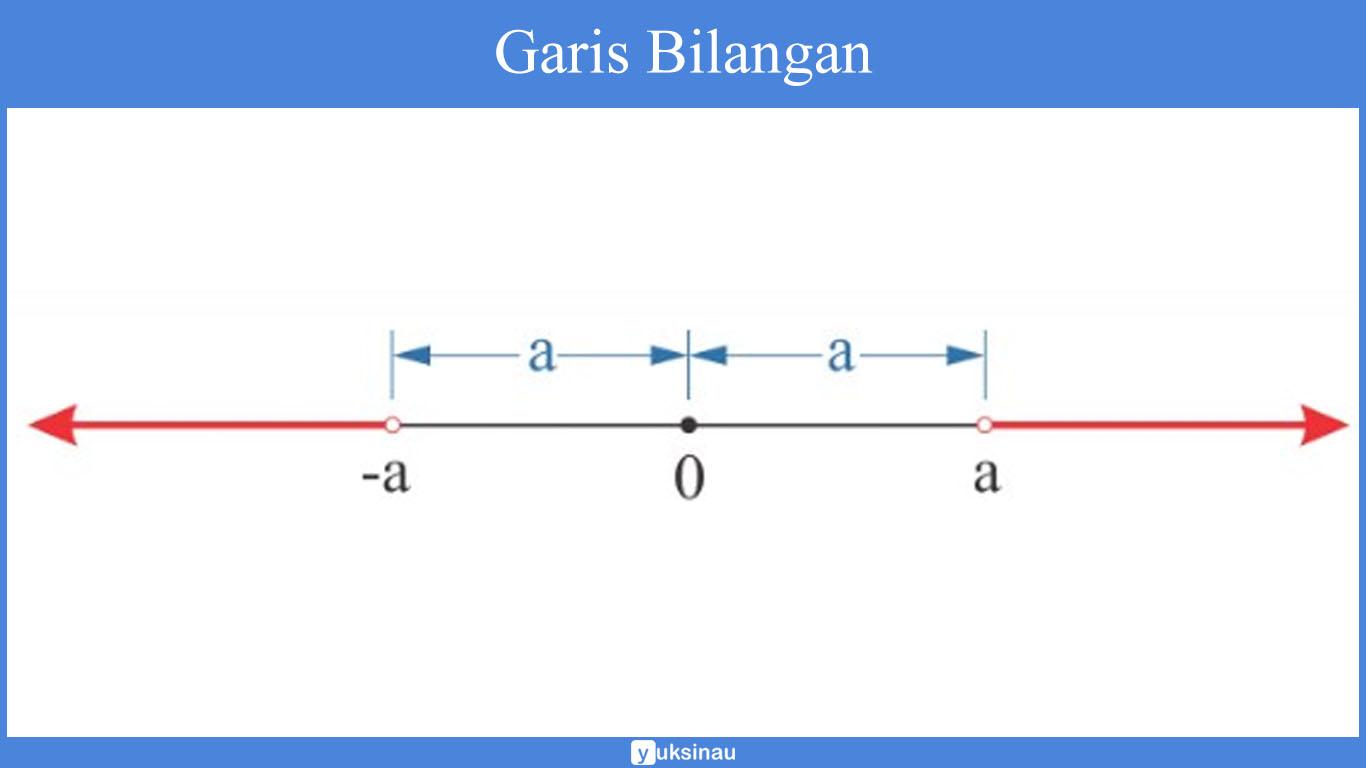
Berdasarkan dari gambar ilustrasi di atas, posisi x digambarkan oleh ruas garis yang berwarna merah, yakni: x < -a atau x > a.
Sehingga, jika kita ambil sembarang titik pada interval tersebut, maka dapat kita pastikan jaraknya ke 0 lebih dari a.
Maka dari itu, supaya jarak x ke nol lebih dari a, haruslah x < -a atau x > a.
Secara intuitif, berbagai uraian di atas bisa kita simpulkan menjadi seperti contoh soal di bawah ini:
Contoh Soal dan Pembahasan
Soal 1.
Tentukanlah suatu himpunan penyelesaian dari: |3x – 7| = 3
Jawab:
Berdasarkan dari sifat a, maka:
|3x – 7| = 3 ⇔ 3x – 7 = 3 atau 3x – 7 = -3
|3x – 7| = 3 ⇔ 3x = 10 atau 3x = 4
|3x – 7| = 3 ⇔ x = 5 atau x = 3
Sehingga, himpunan penyelesaian dari soal 1 adalah HP = {3, 5}.
Soal 2.
Tentukanlah suatu himpunan dari: |3x – 1| = |x + 4|
Jawab:
Berdasarkan dari sifat a, maka:
|3x – 1| = |x + 4|
⇔ 3x – 1 = x + 4 atau 3x – 1 = -(x + 4)
⇔ x = 5 atau 4x = -4
⇔ x = 5 atau x = -1
Sehingga, himpunan penyelesaian dari soal 2 adalah HP = {-1, 5}.
Demikianlah ulasan singkat terkait Persamaan Nilai Mutlak Linier Satu Variabel yang dapat kami sampaikan. Semoga ulasan di atas mengenai Persamaan Nilai Mutlak Linier Satu Variabel dapat kalian jadikan sebagai bahan belajar kalian.
The post Persamaan Nilai Mutlak Linier Satu Variabel appeared first on Tuliskan.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment