Uraian: Irisan Dua Lingkaran (Lengkap)

Irisan Dua Lingkaran - Mungkin banyak diantara kita yang belum tahu tentang sesuatu hal, seperti contohnya informasi mengenai "Irisan Dua Lingkaran?" Lantas berusaha mencari tahu melalui google (internet) dan tanpa sengaja menemukan situs Uraian Lengkap ini. Dapat dikatakan bahwa Anda sudah berada di situs yang tepat, sebab kita memang akan membahas hal tersebut.

Namun tak ada salahnya sebelum membaca ulasan tentang Irisan Dua Lingkaran ada baiknya Anda selaku pembaca, menyimak baik-baik apa yang akan kita kupas dibawah. Seperti pepatah bilang: "Berburu kepadang datar, dapat rusa belang kaki. Berguru kepalang ajar bagai bunga kembang tak jadi". Tentu Anda sudah tahu maksudnya bukan? Oke, langsung ke pembahasannya saja yuk?

Pembahasan Lengkap Irisan Dua Lingkaran

Irisan dua lingkaran merupakan salah satu materi dalam matematik peminatan yang biasanya akan dipelajari pada jenjang kelas 11.

Irisan dua lingkaran ini juga memiliki sebutan lain yaitu irisan dua bundar. Karena bundar sendiri mempunyai makna yang sama dengan lingkaran.

Selengkapnya menenai irisan dua lingkaran, simak baik-baik ulasan di bawah ini.

Penerapan Sifat-sifat Irisan Dua Lingkaran

Sebelum kita mempelajari lebih lanjut mengenai irisan dua bundar/ lingkaran, yuk kita ingat kembali beberapa hal di bawah ini.

Pengertian lingkaran, lingkaran merupakan himpunan titik-titik yang memiliki jarak yang sama terhadap suatu titik tertentu.

Kedudukan Lingkararn

Apabila M1M2 adalah jarak antara dua pusat lingkaran serta r1 dan r2 adalah jari-jari kedua lingkaran, maka :

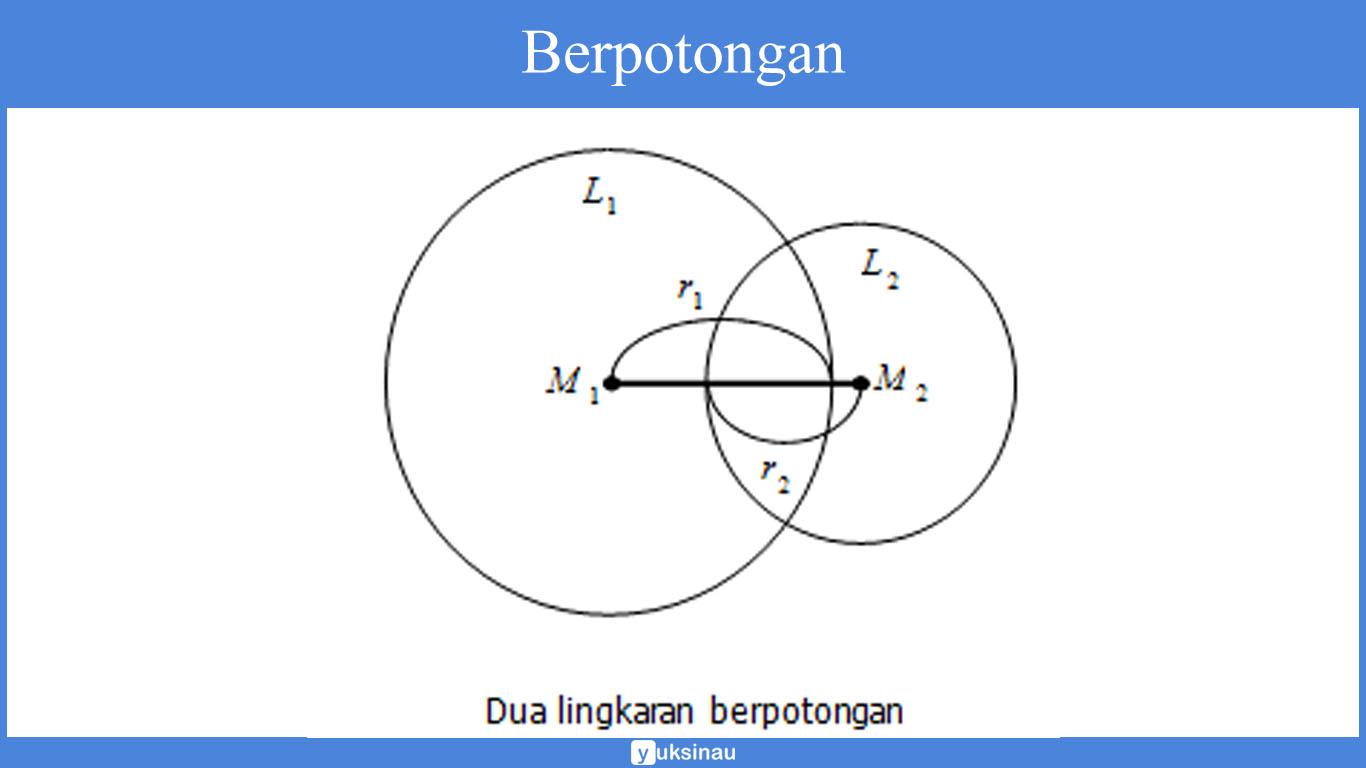
Dua lingkaran disebut berpotongan apabila jarak antara kedua titik pusat lingkaran
M1M2 < r1 + r2

Dua lingkaran disebut sebagai bersinggungan luar apabila jarak antara kedua titik pusat lingkaran adalah M1M2= r1 + r2.

Dua lingkaran disebut bersinggungan dalam apabila jarak antara kedua titik pusat lingkaran adalah M1M2 = |r1 – r2|.

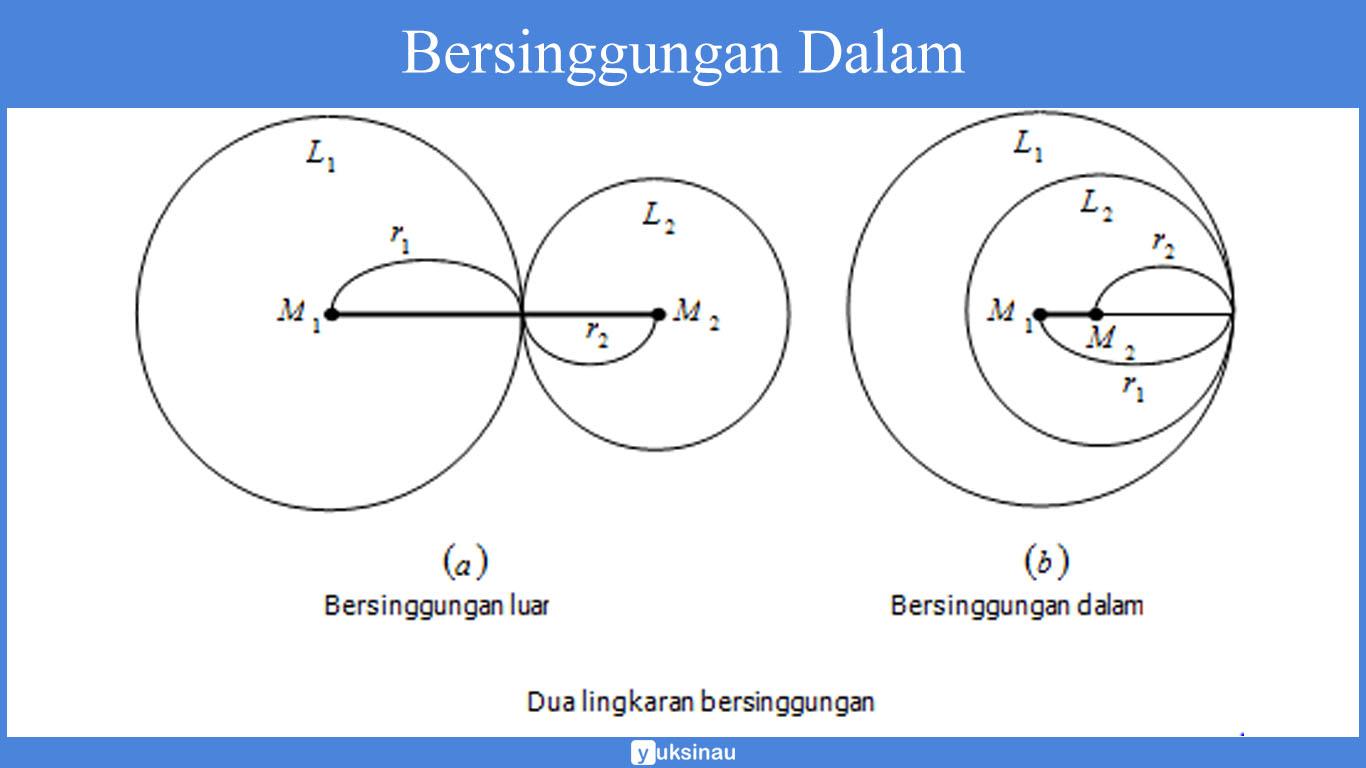
Dua lingkaran disebut tidak saling bersinggungan luar apabila jarak antara kedua titik pusat lingkaran adalah M1M2 > r1 + r2.

Dua lingkaran disebut tidak bersinggungan dalam apabila jarak antara kedua titik pusat lingkaran ialah nol (M1M2 = 0 -> M1 = M2) dan r2 > r1.

Tetapi perlu untuk kalian ketahui juga, dua lingkaran bisa dikatakan tidak bersinggungan dalam apabila salah satu lingkaran terletak di dalam lingkaran yang lain, M1 ≠ M2 dan r2 > r1.

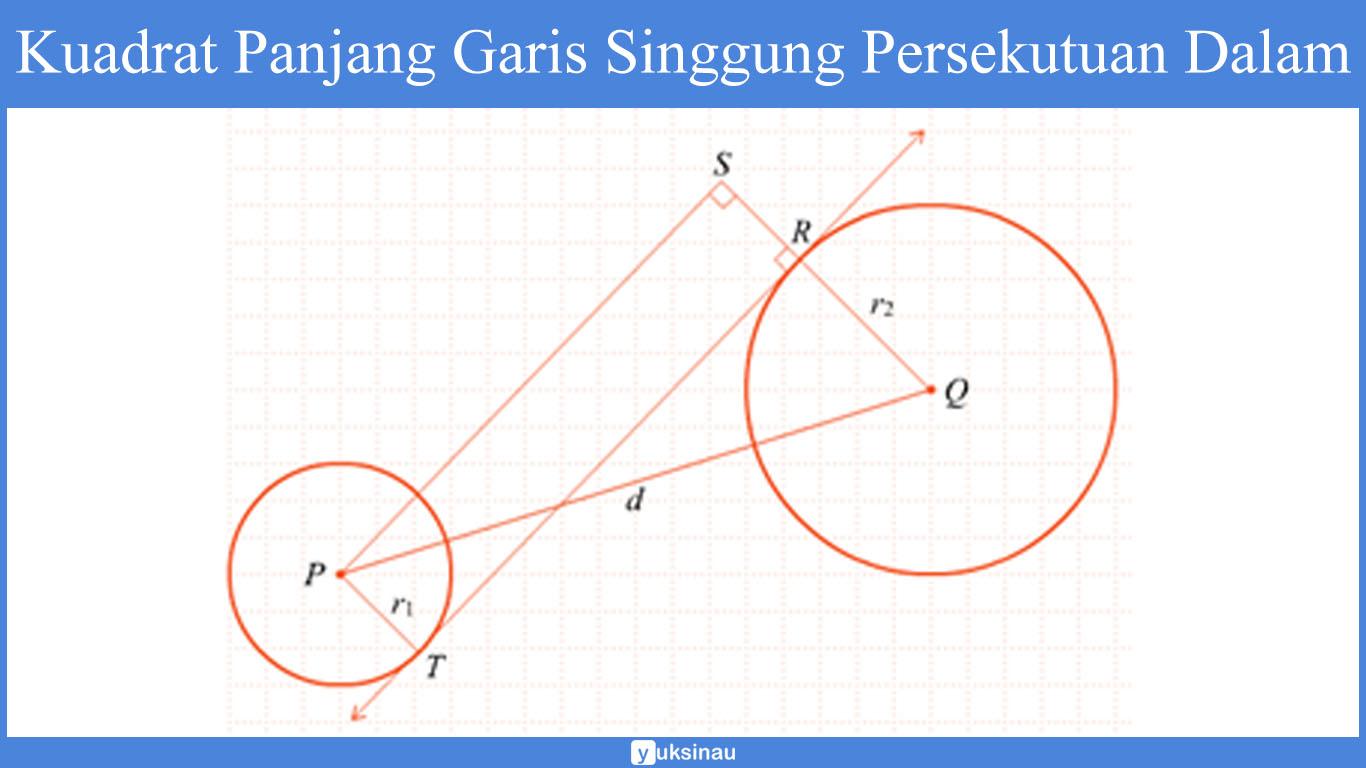
Panjang garis singgung persekutuan dalam merupakan suatu panjang ruas garis yang terbentuk oleh titik-titik singgung lingkaran dengan garis singgung persekutuan dalam.

“Kuadrat dari panjang garis singgung persekutuan dalam lingkaran sama dengan kuadrat yang ada pada jarak titik-titik pusat kedua lingkaran dikurangi dengan kuadrat dari jumlah panjang jari-jarinya”.

Panjang garis singgung persekutuan luar dua lingkaran yang mempunyai jari-jari r1 serta r2 dengan r1 > r2 , dan juga jarak kedua pusat lingkaran d yaitu:

“Kuadrat dari panjang ruas garis singgung persekutuan luar dua lingkaran sama dengan kuadrat yang ada pada jarak titik pusat kedua lingkaran dikurangi dengan kuadrat dari selisih jari-jarinya”.

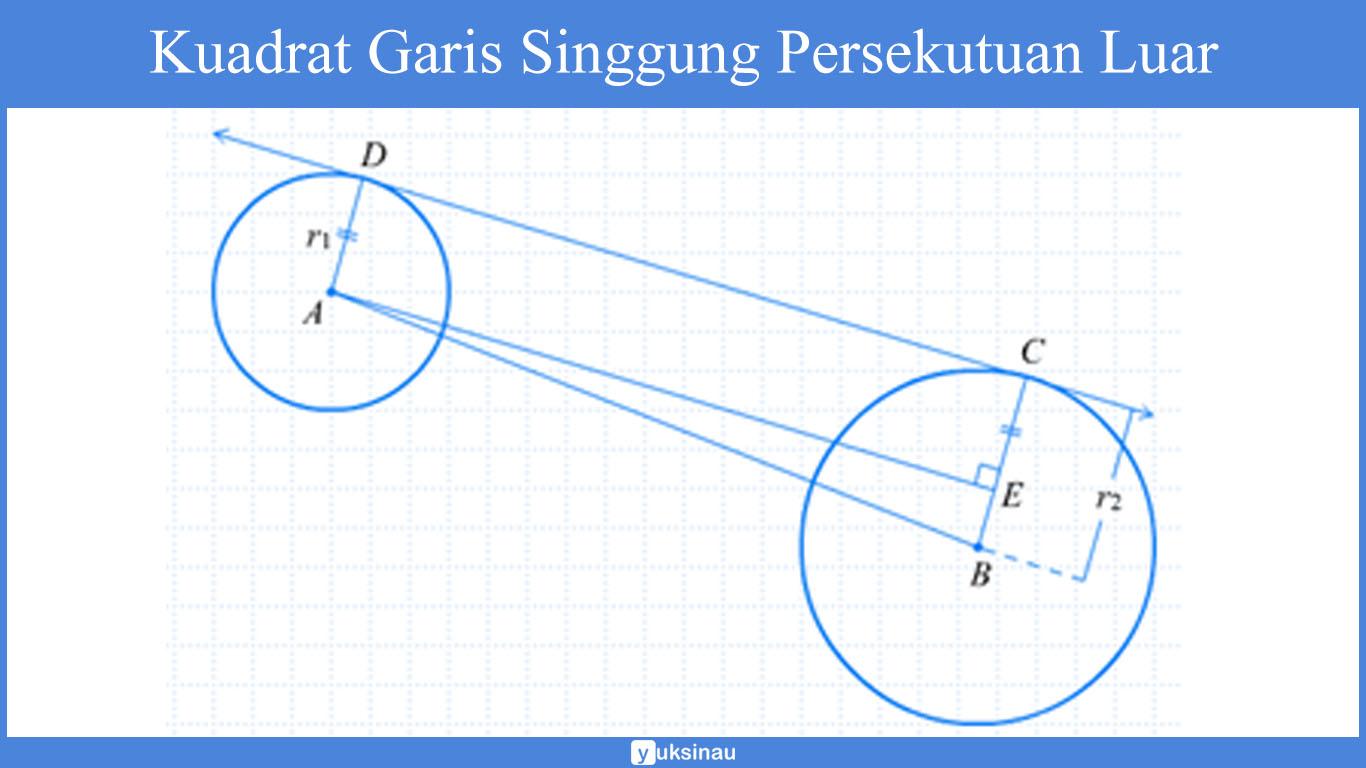
Panjang garis singgung persekutuan dalam dua lingkaran yang mempunyai jari-jari r1 dan r2, dan jarak kedua pusat lingkaran d yaitu:

Baca juga: Perbandingan

Irisan Dua Lingkaran

Apabila M1M2 adalah jarak antara dua sentra bundar serta r1 dan r2 adalah jari-jari kedua lingkaran, maka :

1. Berpotongan

Dua bundar disebut akan saling berpotongan jika jarak antara kedua titik sentra lingkaran adalah M1M2 < r1 + r2.

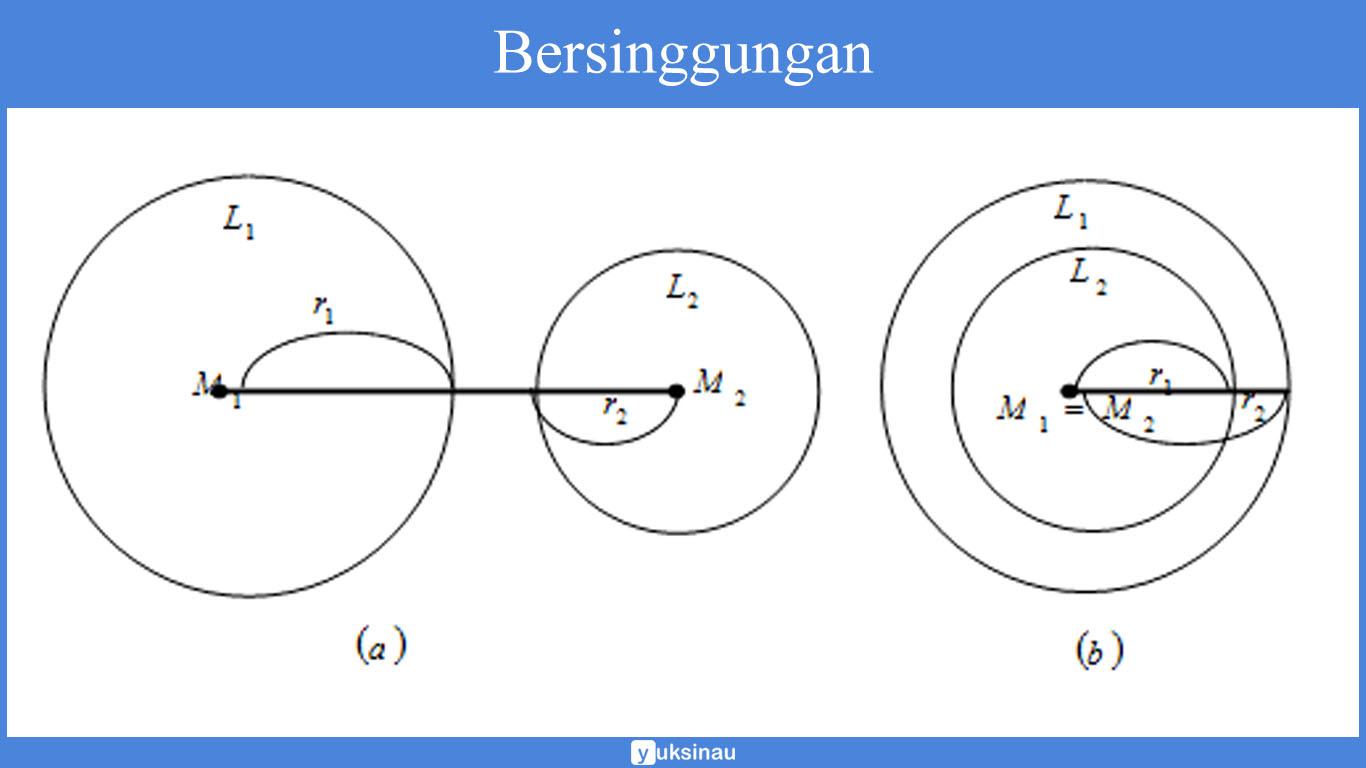
2. Bersinggungan

Dua bundar disebut akan saling bersinggungan luar jika jarak antara kedua titik sentra bundar adalah M1M2= r1 + r2.
Dua bundar disebut akan saling bersinggungan dalam jika jarak antara kedua titik sentra lingkaran adalah M1M2 = |r1 – r2|.

3. Tidak Bersinggungan

Dua bundar dikatakan tidak saling bersinggungan luar jika jarak antara kedua titik sentra lingkaran adalah M1M2 > r1 + r2.

Dua bundar dikatakan tidak saling bersinggungan dalam jika jarak antara kedua titik sentra bundar adalah nol (M1M2 = 0 -> M1 = M2) dan r2 > r1.

Tetapi perlu untuk kalian ketahui juga, dua lingkaran bisa dikatakan tidak bersinggungan dalam apabila salah satu lingkaran terletak di dalam lingkaran yang lain, M1 ≠ M2 dan r2 > r1.

Panjang garis singgung komplotan dalam merupakan panjang ruas garis yang terbentuk oleh titik-titik singgung bundar dengan garis singgung komplotan dalam.

“Kuadrat dari panjang garis singgung komplotan dalam bundar sama dengan kuadrat yang ada pada jarak titik-titik sentra kedua bundar dikurangi dengan kuadrat dari jumlah panjang jari-jarinya”.

Panjang garis singgung komplotan luar dua bundar yang memiliki jari-jari r1 serta r2 dengan r1 > r2 , dan juga jarak kedua sentra bundar d yaitu:

“Kuadrat dari panjang ruas garis singgung komplotan luar dua bundar sama dengan kuadrat yang ada pada jarak titik sentra kedua bundar dikurangi dengan kuadrat dari selisih jari-jarinya”.

Panjang garis singgung komplotan dalam dua bundar yang memiliki jari-jari r1 dan r2, dan juga jarak kedua sentra bundar d adalah:

Untuk lebih mudah memahami uraian di atas, perhatikan beberapa contoh soal sekaligus pembahasan di bawah ini:

Contoh soal.

Soal 1.

Dua buah roda sepeda yang jarak kedua porosnya yaitu 78 cm. Roda pertama mempuyai panjang jari-jari 50 cm, sedangkan roda kedua 20 cm.

Dalam kedua roda dipasang dengan rantai. Hitunglah panjang rantai yang tidak menempel pada roda!

Jawab:

Permasalahan di atas adalah penerapan dari konsep garis singgung persekutuan luar dua lingkaran.

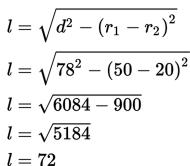
Sehingga, panjang rantai yang tidak menempel pada roda sepeda yaitu 8 cm.

Soal 2.

Terdapat 8 buah tabung disusun seperti yang ada pada gambar di bawah. Lalu tabung tersebut diikat dengan menggunakan seutas tali.

Apabila panjang jari-jari tabung 14 cm, maka hitunglah panjang tali terpendek yang dipakai untuk mengikat tabung-tabung tersebut!

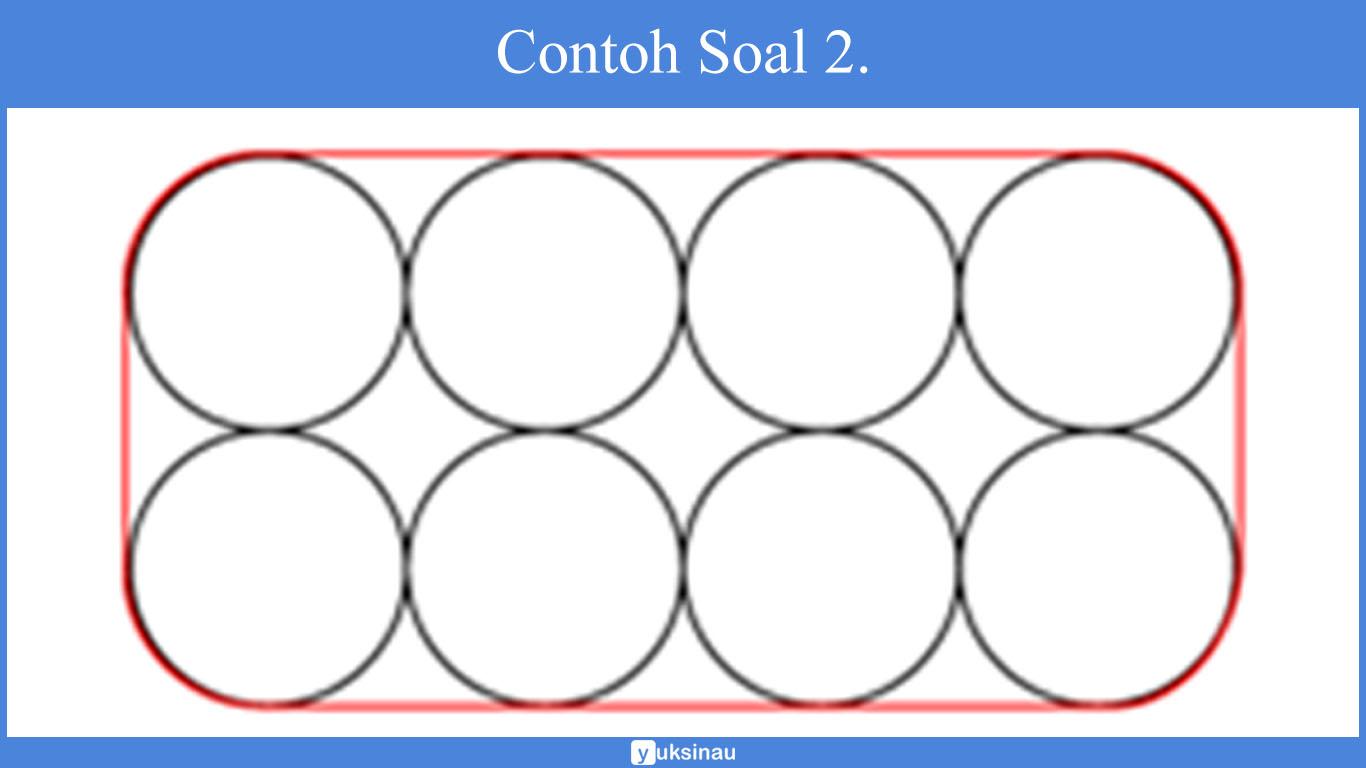
Jawab:

Diketahui:

• Jarak pusat dua lingkaran adalah  = diameter lingkaran = 28 cm
• Jumlah panjang tali di sudut-sudut tabung adalah = keliling lingkaran = πd = 88 cm

Sehingga, panjang tali terpendek yang dipakai untuk mengikat tabung yaitu:

(8 x 28 cm) + 88 cm = 312 cm

Soal 3.

Terdapar dua buah lingkaran pada bidang yang memiliki titik pusat yang sama. Jari-jari lingkaran besar yaitu empat kali jari-jari lingkaran kecil.

Apabila luas daerah di antara kedua lingkaran sebesar 8 satuan luas, maka tentukanlah luas daerah lingkaran kecil!

Jawab:

Misalnya jari-jari lingkaran besar adalah = R serta jari-jari lingkaran kecil adalah = r , maka akan kita dapatkan :

R = 4r

Dengan begitu:

Luas = Lbesar – Lkecil
8  = πR² – πr²
8 = π(4/r – πr²
8 = 16πr² – πr²
8 = 15πr²
πr² = 8/15
Lkecil = 8/15

Sehingga, luas daerah lingkaran kecil adalah 8/15 satuan luas.

Baca juga: Bangun Datar (Gabungan)

Soal 4.

Pak Gilang tengan membuat kerangka suatu gerobak seperti yang ada pada gambar di bawah ini.

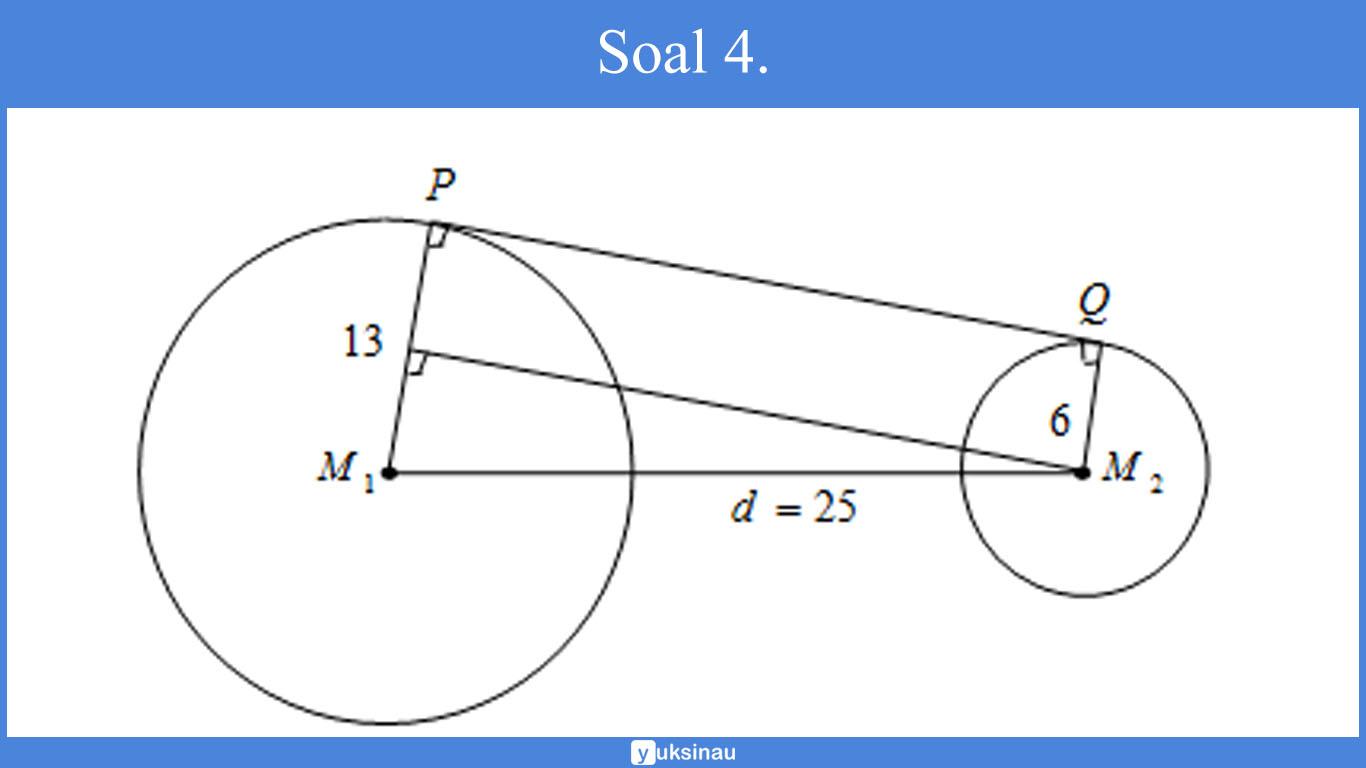
Pada salah satu sisi gerobak tersebut terdapat suatu papan berbentuk trapesium yang mengaitkan kedua roda gerobak.

Jika jari-jari roda yang besar yaitu r1 = 13 cm, jari-jari roda yang kecil yaitu r2 = 6 cm, jarak titik pusat roda L1 serta roda L2 adalah M1M2 = 25 cm. Maka hitunglah luas papan yang menghubungkan kedua roda tersebut!

Jawab:

Langkah pertama adalah menghitung terlebih dahulu panjang garis singgung persekutuan luar PQ. Dengan cara:

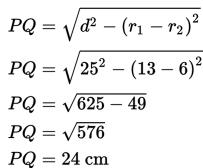
Adapun luas trapesium PM1M2Q ialah sebagai berikut:

Luas = jumlah sisi sejajar x tingg/ 2
Luas = (13+6)x 24/ 2
Luas = 19×24/ 2
Luas = 228 cm²

Sehingga, luas papan penghubung kedua roda tersebut adalah 228 cm²

Penerapan Konsep IDL dalam Masalah Kehidupan Sehari-hari

Jam dinding, ban mobil, serta mata uang logam adalah beberapa contoh benda-benda yang mempunyai bentuk dasar lingkaran.

Dalam bab sebelumnya, kalian sudah mempelajari sekaigus mengenal mengenai irisan kerucut yang terdiri dari kurva-kurva parabola, elips dan juga hiperbola.

Tetapi, dalam berbagai bentuknya yang istimewa kita juga akan mendapatkan suatu lingkaran dalam irisan kerucut.

Dalam irisan kerucut, lingkaran terbentuk sebab dalam bidang datar mengiris semua bagian dari salah satu selimut kerucut serta tegak lurus pada sumbu kerucut.

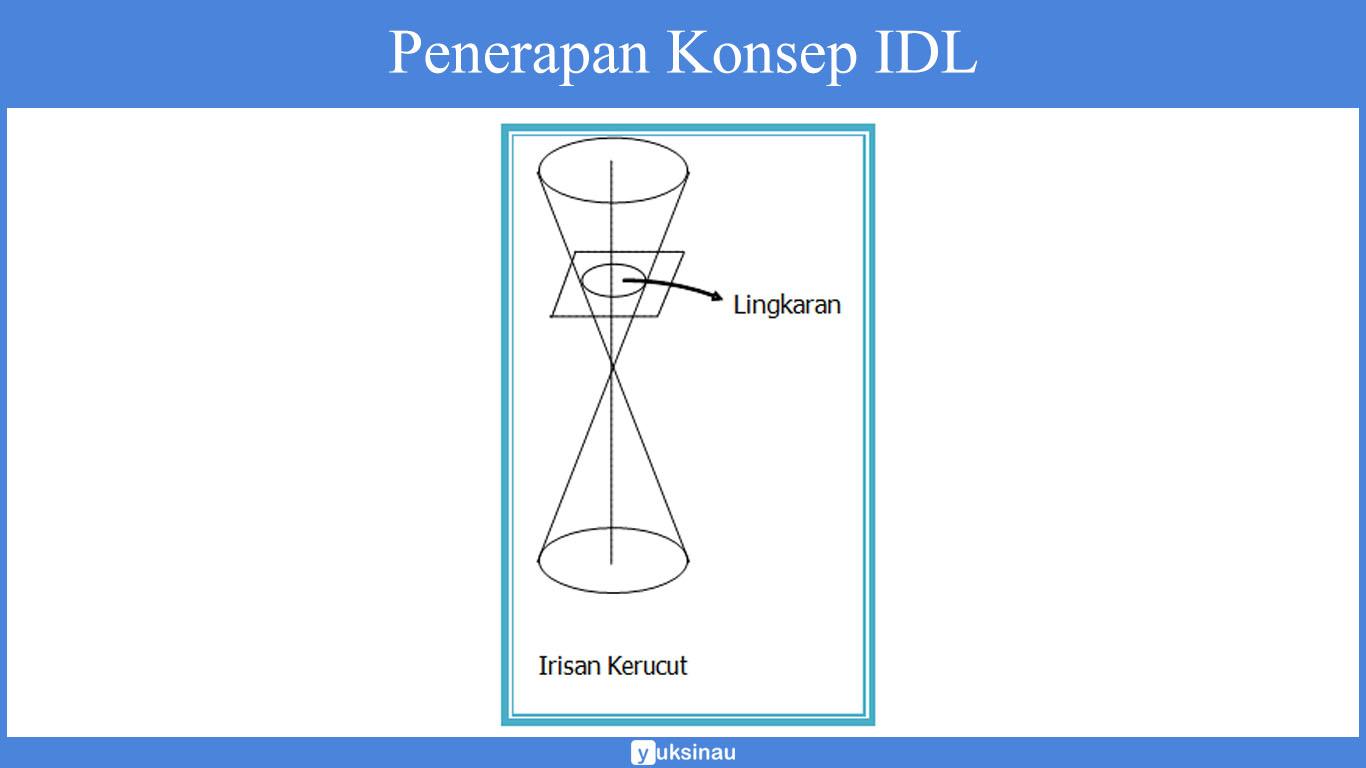
Mari kita ingat kembali pengertian dari lingkaran. Seperti yang telah di jelaskan di atas, lingkaran merupakan suatu himpunan titik-titik yang berjarak sama pada suatu titik tertentu.

Tak hanya itu, tentunya kalian juga sudah mempelajari topik mengenai kedudukan dua lingkaran. Untuk menyegarkan ingatan kalian mengenai topik tersebut, yuk simak ulasan materi di bawah ini.

1. Kedudukan dua lingkaran

Misalnya M1M2 adalah jarak antara dua pusat lingkaran dan r1 serta r2 adalah jari-jari kedua lingkaran, maka akan berlaku:

Dua lingkaran disebut akan saling berpotongan apabila jarak antara kedua titik pusat lingkaran adalah M1M2 < r1 + r2.

Dua lingkaran disebut akan saling bersinggungan luar apabila jarak antara kedua titik pusat lingkaran M1M2= r1 + r2.

Dua lingkaran disebut akan saling bersinggungan dalam apabila jarak antara kedua titik pusat lingkaran adalah M1M2 = |r1 – r2|.

Dua lingkaran disebut tidak akan saling bersinggungan luar apabila jarak antara kedua titik pusat lingkaran adalah M1M2 > r1 + r2.

Dua lingkaran disebut tidak akan saling bersinggungan dalam apabila jarak antara kedua titik pusat lingkaran ialah  nol (M1M2 = 0 -> M1 = M2) dan r2 > r1.

Tetapi perlu untuk kalian ketahui juga, dua lingkaran bisa dikatakan tidak bersinggungan dalam apabila salah satu lingkaran terletak di dalam lingkaran yang lain, M1 ≠ M2 dan r2 > r1.

Panjang garis singgung persekutuan luar dua bundar yang memiliki jari-jari r1 serta r2 dengan r1 > r2 , dan juga jarak kedua sentra bundar d yaitu:

Panjang garis singgung komplotan dalam dua bundar yang memiliki jari-jari r1 dan r2, dan juga jarak kedua sentra bundar d adalah:

persekutuan dalam

Contoh Soal dan Pembahasan

Untuk mempermudah pemahaman kalian, berikut akan kami berikan beberapa contoh soal sekaligus pembahasannya untuk kalian semua.

Soal 1.

Diketahui suatu persamaan lingkaran di bawah ini:

• L1: x² + y² + 8x + 6y – 56 = 0 
• L2: x² + y² – 8x – 6y – 24 = 0 

Tunjukkan jika kedua lingkaran tersebut saling berpotongan!

Jawab:

Syarat dua lingkaran akan saling berpotongan yaitu apabila jarak antara kedua titik pusat lingkaran lebih kecil dari jumlah kedua jari-jari lingkaran.

Sebagai contoh:

M1M2 adalah jarak antara dua pusat lingkaran dengan r1 serta r2 merupakan jari-jari kedua lingkaran, maka M1M2 < r1 + r2.

L1: x² + y² + 8x + 6y – 56 = 0

Memiliki pusat M1(-1/2 A , -1/2 B) = (-1/2 (8) , -1/2 (6)) = (-4, -3) dan;

L2: x² + y² – 8x – 6y – 24 = 0

Memiliki pusat M2(-1/2 A , -1/2 B) = (-1/2 (-8) , -1/2 (-6)) = (4,3) serta;

 

 

M1M2 adalah jarak dari (-4 , -3) ke (4,3).

Sebab r1 + r2 = 9 + 7 = 16 dan juga M1M2 = 10, maka M1M2 < r1 + r2.

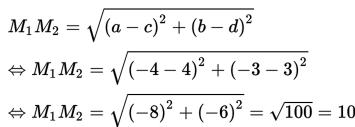
Dengan begitu, kedua lingkaran tersebut terbukti saling berpotongan.

Soal 2.

Diketahui persamaan lingkaran

• L1: x² + y² + 6x – 4y – 23 = 0 
• L2: x² + y² – 12x + 20y + 55 = 0 

Buktikan jika lingkaran saling bersinggungan di luar!

Jawab:

Syarat dua lingkaran bersinggungan di luar yaitu M1M2 = r1 + r2.

L1: x² + y² + 6x – 4y – 23 = 0

Memiliki pusat M1(-1/2 A , -1/2 B) = (-1/2 (6) , -1/2 (-4)) = (-3, 2) serta;

L2: x² + y² – 12x + 20y + 55 = 0

Memiliki pusat M2(-1/2 A , -1/2 B) = (-1/2 (-12) , -1/2 (20)) = (6 , -10) serta;

M1M2 adalah jarak dari (-3 , 2) ke (6 , -10). Sehingga:

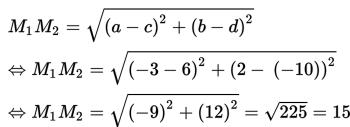
Sebab, r1 + r2 = 6 + 9 = 15 = M1M2 maka kedua lingkaran tersebut terbukti bersinggungan di luar.

Soal 3.

Diketahui persamaan lingkaran

• L1: x² + y² + 20x – 12y + 72 = 0 
• L2: x² + y² – 4x – 2y – 11 = 0 

Buktikan jika kedua lingkaran tidak saling berpotongan!

Jawab:

L1: x² + y² + 6x – 4y – 23 = 0

Memiliki pusat M1(-1/2 A , -1/2 B) = (-1/2 (20) , -1/2 (-12)) = (-10, 6) serta;

L2: x² + y² – 4x – 2y – 11 = 0

Memiliki pusat M2(-1/2 A , -1/2 B) = (-1/2 (-4) , -1/2 (-2)) = (2,1) serta;

Terdapat dua jenis lingkaran yang disebut tidak saling berpotongan, yakni:

1. dua lingkaran tidak berpotongan luar dengan M1M2 > r1 + r2 
2. dua lingkaran tidak berpotongan dalam (sepusat atau jarak antara dua titik pusat lingkaran (M1M2) merupakan nol ⟺ M1 = M2 dan r1 > r2 serta tidak sepusat).

Sekarang, kita akan membuktikan titik pusat dari kedua lingkaran tersebut untuk menunjukkan kedua lingkaran tersebut tidak saling berpotongan luar atau tidak berpotongan dalam.

Titik pusat lingkaran pertama pada lingkaran kedua.

Substitusi pusat (-10,6) pada lingkaran L2: x² + y² – 4x – 2y – 11 = 0

Adapun syarat untuk titik berada di dalam lingkaran yaitu K < 0.

Sebab

K = (-10)2 + 62 – 4(-10) – 2(6) – 11 = 100 + 36 + 40 – 12 – 11 = 153 > 0 

Sehingga, pusat lingkaran pertama terletak di luar lingkaran kedua. Titik pusat lingkaran kedua pada lingkaran pertama.

Substitusi pusat (2,1) pada lingkaran L1 : x2 + y2 + 20x – 12y + 72 = 0

Syarat untuk titik terletak di dalam lingkaran yaitu K < 0.

Sebab, 

K = 22 + 12 + 20(2) – 12(1) + 72 = 4 + 1 + 40 – 12 + 72 = 103 > 0 

Sehingga, pusat lingkaran pertama terletak di luar lingkaran pertama.

Sehingga, bisa kita simpulkan jika kedua lingkaran tidak akan saling berpotongan dalam, kemudian akan kita buktikan juga jika kedua lingkaran tersebut tidak saling berpotongan luar.

Syarat dua lingkaran tidak berpotongan luar ialah: M1M2 > r1 + r2

M1M2 adalah jarak dari (-10,6) ke (2,1).

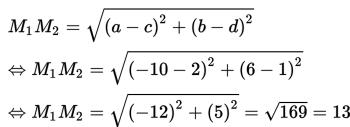
Sebab,

M1M2 = 13
r1 + r2 = 8 + 4 = 12

Sehingga, M1M2 > r1 + r2

Dengan begitu, terbukti bahwa kedua lingkaran tidak saling berpotongan di luar.

Soal 4.

Diketahui terdapat jari-jari lingkaran L1 adalah r1 = 13cm serta jari-jari L2 yakni r2 = 6cm.

Apabila jarak titik pusat kedua lingkaran ialah M1M2 = 25cm. Maka hitunglah panjang garis singgung persekutuan luar dari kedua lingkaran tersebut!

Jawab:

Diketahui:

• r1 = 13cm
• r2 = 6cm
• M1M2 = 25cm

Ditanyakan:

• panjang garis singgung persekutuan luar PQ

Penyelesaian:

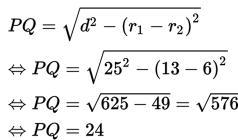
Sehingga, panjang garis singgung persekutuan luar dari kedua lingkaran yaitu 24 cm.

Baca juga: Polinomial

Demikianlah ulasan singkat terkait Irisan Dua Lingkaran yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.

The post Irisan Dua Lingkaran appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Jika Anda sudah membaca kalimat ini, maka Anda sudah sampai dibagian akhir pembahasan tentang Uraian: Irisan Dua Lingkaran (Lengkap). Semoga saja uraian kami diatas dapat menjawab rasa penasaran Anda dan menambah wawasan untuk kita semua. Tak lupa kami sampaikan banyak terima kasih sudah berkunjung ke situs uraian lengkap ini. Sampai jumpa di postingan selanjutnya.